De vez en cuando, algún periódico en su sección de "noticias de ciencia" se descuelga con informaciones sobre un experimento que ha logrado teletransportar un átomo cierta distancia. Pues sintiédolo mucho, va a ser que no. Nada de mover cosas de un sitio a otro en un parpadeo. Se trata de teleportación cuántica, que pese a su (desafortunado) nombre, es algo bastante diferente.
jueves, 31 de diciembre de 2015
martes, 8 de diciembre de 2015
El secreto está en la masa
La masa... ese concepto tan familiar y a la vez tan profundo. ¿Qué entendemos por masa, y de dónde surge? Son preguntas más difíciles de lo que parece. Espero arrojar un poco de luz, y no liarlo todo más.
lunes, 30 de noviembre de 2015
Hasta el infinito... y más acá
Hasta ahora nos habíamos preocupado, mirando las métricas y la curvatura, lo que ocurre en un espaciotiempo a escala local. Pero si miramos un poco más lejos veremos que aún pasan cosas interesantes.
miércoles, 25 de noviembre de 2015
En busca del gravitón perdido
En los años en los que se estaba gestando la Relatividad General también había surgido una teoría que había revolucionado por completo la física: la mecánica cuántica. En unos pocos años, se conseguiría una descripción cuántica completa de las tres interacciones no gravitatorias (electromagnética, fuerte y débil). Pero la gravedad se resistía, y se sigue resistiendo, a ser cuántica.
Y tiene que serlo. Ya en 1916 Einstein expresó esta necesidad: un electrón en un átomo, clásicamente, esta acelerando, y por tanto debería perder energía emitiendo ondas electromagnéticas y gravitatorias hasta finalmente caer al núcleo. Como la radiación electromagnética está cuantizada en fotones, el electrón solo puede emitir ondas electromagnéticas al pasar de nivel energético. Para que el átomo sea estable, lo mismo debería pasar con la emisión de ondas gravitatorias.
sábado, 21 de noviembre de 2015
Relatividad General en la cresta de la onda
En la Relatividad General, los efectos gravitatorios no se transmiten como una acción a distancia. En su lugar, los cambios de curvatura espaciotemporal, y la energía y momento lineal asociados, se transmiten a una velocidad limitada. Einstein propuso en 1916 la existencia de ondas gravitacionales, "ondulaciones" en la métrica del espaciotiempo. Desde entonces se ha estado buscando incansablemente estas ondas gravitacionales, con mayor o menor fortuna.
lunes, 16 de noviembre de 2015
Un Universo a mi medida
¿Por qué limitarse a estudiar los efectos gravitatorios de una estrella, como había hecho Schwarzschild? La nueva ecuación de Einstein permitía describir la forma y dinámica del Universo en su conjunto. Con la relatividad general nació la cosmología como ciencia.
miércoles, 11 de noviembre de 2015
Cualquier agujero negro es trinchera
La ecuación de campo de Einstein, una vez que se plantea para una geometría determinada, se convierte en un conjunto de diez ecuaciones diferenciales de segundo grado no lineales acopladas. Sí, da tanto miedo como aparenta. Tanto es así que Einstein para sus predicciones había empleado solamente una aproximación, y creía que era completamente imposible encontrar una solución exacta a su portentosa ecuación.
viernes, 6 de noviembre de 2015
La idea más feliz de Einstein
Einstein había descubierto en 1905 la Relatividad Especial. De las dos fuerzas que se conocían en aquella época, el electromagnetismo era perfectamente compatible con la nueva teoría, no así la gravitación.Por un lado, se describía como una interacción a distancia (lo que ya dejó insatisfecho a Newton) desafiando el límite de la velocidad de la luz. Además la causa de la gravedad era la masa, que en relatividad especial no es más que una forma de energía.
domingo, 1 de noviembre de 2015
Teatro de variedades (riemannianas)
Aquí comienza la serie de entradas dedicadas a conmemorar el centenario de la teoría de la Relatividad General. Pero vamos a empezar la historia un poco antes...
Es una cálida tarde de verano, alrededor del 300 a.C. Has terminado tus compras en el mercado local o "ágora", y empiezas a leer el último bestseller: los Elementos, escrito por Euclides. Todo lo que siempre quisiste saber sobre geometría pero nunca te atreviste a preguntar. Todo a partir de solo cinco postulados:
- Dos puntos cualesquiera determinan un segmento de recta.
- Un segmento de recta se puede extender indefinidamente en una línea recta.
- Se puede trazar una circunferencia dados un centro y un radio cualquiera.
- Todos los ángulos rectos son iguales entre sí.
- Por un punto exterior a una recta, se puede trazar una única paralela.
Todo parece muy lógico. Pero hay algo extraño en el último postulado, no acaba de encajar con los demás. Durante más de mil años intrigó a matemáticos de distintas culturas, que intentaron deducirlo del resto de postulados. Pero una y otra vez fallaban. La existencia de paralelas tenía que ser una suposición adicional, y era posible construir geometrías alternativas sin ella.
Gauss fue probablemente el mayor matemático de todos los tiempos. Uno de sus intereses fue las propiedades intrínsecas de las superficies (las que podría medir un planilandés que viviera en ella), lo que hoy llamamos geometría diferencial. Seguramente esto le llevaría a la idea de acabar con el quinto postulado. Pero Euclides era mucho Euclides, incluso para Gauss, así que no se atrevió a publicarlo. En su lugar "empleó" para tan revolucionaria misión a su alumno, Riemann. Así que la generalización de la geometría sin este postulado se conoce como geometría riemanniana.
 |
| Gauss (izquierda) y Riemann (derecha) |
El objeto principal es la variedad riemanniana. Una variedad es básicamente la generalización de una curva o una superficie. Es un conjunto de puntos tales que las proximidades de cada punto se parecen a un espacio vectorial \(\mathbb{R}^N\). Los vectores que viven en ese espacio son vectores tangentes en dicho punto.
Si tenemos vectores, ya podemos empezar a medir distancias y ángulos. Para ello necesitamos tener un producto escalar. A veces (casi siempre) las coordenadas cartesianas serán un incordio para operar. Por ello, usaremos un producto escalar que no dependa de la elección de coordenadas, usando la métrica \(g\): \[\vec{v}\cdot\vec{w} = \sum_{ij} g_{ij}v^i w^j \equiv g_{ij}v^i w^j\]
La métrica en general dependerá de las coordenadas, con lo cual la medida de distancias y ángulos depende de la posición. Esto no debe sorprendernos: por ejemplo, la distancia entre dos meridianos es mayor en el Ecuador que en el Círculo Polar.
 |
| La longitud del segmento rojo es mayor que la del segmento verde, aunque la diferencia de coordenadas (esféricas) entre los extremos sea igual en ambos casos. |
Todo esto funciona para las propiedades locales de la variedad, las que dependen de los vectores tangentes en un único punto. Ahora tenemos que preocuparnos por las propiedades globales, y para ello necesitaremos algo que conecte los espacios de vectores tangentes en puntos diferentes. En \(\mathbb{R}^N\) puede parecer muy sencillo, pero en una variedad general no lo es. Para ello hace falta un nuevo ingrediente: la conexión \(\Gamma\). En principio, hay libertad total para elegir esta conexión, aunque hay una en especial, la conexión de Levi-Civita, que es más natural ya que se construye a partir de la métrica.
 |
| Espacios tangentes (rojo) en dos puntos de una variedad (azul), relacionados mediante una conexión (curva rosa) |
Ya podemos trasladarnos de un punto a otro de la variedad. Vamos a hacer un transporte paralelo: recorreremos una curva cerrada portando un vector, pero con cuidado de no girarlo en ningún momento. Si hacemos este ejercicio en un plano, nada extraño ocurre, y al volver al punto de origen el vector apunta en la misma dirección que al principio. ¿Y si lo hacemos en una esfera? Partamos de un punto sobre el Ecuador, con el vector señalando hacia el norte. Avanzamos en dirección norte por un meridiano hasta el polo. A continuación vamos en dirección sur por otro meridiano distinto hasta el Ecuador. Finalmente volvemos al punto de partida siguiendo el Ecuador ¿A que ahora el vector ha cambiado de dirección? Este efecto se llama curvatura.
 |
| Transporte paralelo en una esfera. |
Volviendo al inicio de esta entrada, la curvatura también es responsable de la derogación del quinto postulado de Euclides. Una curva geodésica es la trayectoria que presenta la mínima distancia entre dos puntos. Si la variedad posee curvatura, dos geodésica próximas pueden acercarse o alejarse. Del mismo modo, en un triángulo formado por tres geodésicas la suma de los ángulos es distinta de 180° si hay curvatura.
Matemáticamente la curvatura se cuantifica mediante el tenor de Riemann \( {R^\mu}_{\nu\rho\sigma}\). También son útiles para describir la curvatura otras cantidades, calculadas a partir del tensor de Riemann: el tensor de Ricci \(R_{\mu\nu}\), el escalar de curvatura \(R\) y el tensor de Einstein \(G_{\mu\nu}\). Como muchos habréis adivinado, el tensor de Einstein jugará un papel fundamental en la Relatividad General.
sábado, 31 de octubre de 2015
Celebrando el centenario de la Relatividad General
En el mes de noviembre se cumplen los 100 años de que Albert Einstein propusiera la teoría de la Relatividad General, el paradigma utilizado actualmente para describir la gravitación. Para conmemorarlo, a lo largo de este mes vamos a dedicarlo a esta teoría y algunas de sus aplicaciones:
- Geometría Riemanniana 1/11: Teatro de variedades (riemannianas)
- La ecuación de Einstein 6/11: La idea más feliz de Einstein
- Agujeros negros 11/11: Cualquier agujero negro es trinchera
- Cosmología FLRW 16/11: Un Universo a mi medida
- Radiación gravitacional 21/11: Relatividad General en la cresta de la onda
- GR vs QFT 25/11: En busca del gravitón perdido
martes, 13 de octubre de 2015
Un ordenador a base de mover rocas
Si estás leyendo esto, estarás usando un ordenador o similar (móvil, tablet,... o quien sabe, quizás la pantalla de una lavadora de última tecnología). Pero, ¿qué es, realmente, un ordenador?
martes, 6 de octubre de 2015
¿Muónicos? Yo había encargado neutrinos electrónicos
Octubre ha llegado, y con él el anuncio de los premios Nobel de este año. En la categoría de física, el honor ha recaído en Takaaki Kajita y Arthur B. "Art" McDonald, directores de dos observatorios de neutrinos, Super-Kamiokande y SNO. Su labor ha permitido detectar experimentalmente un fenómeno conocido como oscilación de neutrinos.
lunes, 5 de octubre de 2015
Primer cumpleblog
Parece como si hubiera sido ayer. Pero ya hace un año desde que comencé a escribir este blog. Originalmente la idea era ir escribiendo un poco lo que se me fuera ocurriendo sobre la marcha, y que un número reducido de personas (familia y amigos principalmente) lo leyeran... si se atrevían.
Pero por avatares del destino, el blog ha llegado bastante más lejos de lo que nunca habría imaginado. Lo han leído desde más de cien países y desde todos los continentes. Las entradas suelen tener varios centenares de visitas, y he conseguido algún que otro lector incondicional. Todo esto me causa orgullo, por supuesto, pero también una cierta dosis de responsabilidad, incluso vértigo, ya que un artista se debe a su público.
En los últimos días, en el plano personal he estado viviendo bastantes cambios. Seguramente tendrán cierta repercusión en el blog, tanto en la periodicidad como en la temática de las entradas. Pero no os preocupéis, que hay algunos posts cociéndose en el horno.
Para conmemorar este cumpleblog, he reeditado la primera entrada que escribí en formato cómic (para que podáis admirar mis prácticamente nulas dotes de dibujo ;)). Lo tenéis en pdf y cbz.
Muchas gracias a todos por este maravilloso año.
Pero por avatares del destino, el blog ha llegado bastante más lejos de lo que nunca habría imaginado. Lo han leído desde más de cien países y desde todos los continentes. Las entradas suelen tener varios centenares de visitas, y he conseguido algún que otro lector incondicional. Todo esto me causa orgullo, por supuesto, pero también una cierta dosis de responsabilidad, incluso vértigo, ya que un artista se debe a su público.
En los últimos días, en el plano personal he estado viviendo bastantes cambios. Seguramente tendrán cierta repercusión en el blog, tanto en la periodicidad como en la temática de las entradas. Pero no os preocupéis, que hay algunos posts cociéndose en el horno.
Para conmemorar este cumpleblog, he reeditado la primera entrada que escribí en formato cómic (para que podáis admirar mis prácticamente nulas dotes de dibujo ;)). Lo tenéis en pdf y cbz.
Muchas gracias a todos por este maravilloso año.
martes, 22 de septiembre de 2015
Reseña: The Clockwork Rocket, de Greg Egan
Hay muchos tipos de ciencia-ficción: desde space operas de serie Z donde los fáseres sustituyen a los revólveres de los cowboys de antaño hasta geniales distopías que nos advierten de los vicios de nuestra sociedad. Pero Greg Egan juega en otra liga. En sus novelas, la ciencia más dura juega un papel tan importante como los protagonistas (o más), y cuida exquisitamente cada detalle.
martes, 8 de septiembre de 2015
Condensador de fluzo... fluceando
La entrada de hoy va a ser un poco diferente a la tónica general de este blog. Toca un poco de desmadre, porque vamos a adentrarnos en el terreno de la ciencia ficción, aunque sin dejar de lado la física. Vamos a hablar de viajes en el tiempo.
Taquiones
La relatividad especial establece que si una partícula viajara más rápido que la luz, en algunos sistemas de referencia sería vista como una partícula que viaja hacia atrás en el tiempo. Así lo ilustra el siguiente diagrama espaciotemporal. En rojo se ilustra un viaje supralumínico según el observador \(O\) (ejes \(x\) y \(t\), en línea continua): El punto de origen se encuentra en su presente y el destino en su futuro pero fuera del cono de luz (región sombreada en azul). Por el contrario, para el observador \(O'\) (ejes \(x'\) y \(t'\), en línea discontinua), el punto "final" del viaje se produce en un momento anterior en su tiempo que el inicio.
Claro que la relatividad especial también prohibe que una partícula con masa acelere hasta la velocidad de la luz, o que una partícula sin masa vaya a una velocidad diferente de \(c\).
Pero aún hay una esperanza: partículas con masa imaginaria, llamadas taquiones. La energía de una partícula con velocidad \(v\) es \[E = \frac{mc^2}{\sqrt{1-\frac{v^2}{c^2}}}\]Si la partícula excede la velocidad de la luz, tendríamos la raíz cuadrada de un número negativo, con lo que la masa también tiene que ser imaginaria para que la energía sea real y la expresión tenga sentido. Al igual que las partículas "normales" no pueden rebasar la velocidad de la luz, los taquiones no pueden ir más despacio.
Por supuesto, los taquiones según la descripción anterior son un concepto puramente ficticio. Sin embargo, en teoría cuántica de campos sí que existen campos taquiónicos con masa imaginaria. Estos campos no permiten superar la velocidad de la luz, sino que dan lugar a inestabilidades que terminan en forma de transiciones de fase (condensación). Los campos taquiónicos juegan un papel importante en el mecanismo de Higgs y en la superconductividad.
CTC's
Ya que la relatividad especial no ofrece perspectivas muy halagüeñas, pasemos a la relatividad general. En esta teoría, la concentración de masa y/o energía en un punto determina la geometría en sus proximidades. ¿Nos permitirá una geometría suficientemente enrevesada viajar en el tiempo?
Una curva temporal cerrada (CTC) es una trayectoria a lo largo de un espaciotiempo curvo que regresa a su origen. La mayor parte de las soluciones a la ecuación de Einstein, incluyendo las que se emplean habitualmente nuestro Universo, no las permiten, pero hay algunas excepciones curiosas. La primera fue encontrada por Gödel, y describe un universo con constante cosmológica y lleno de "polvo" rotando. Otro ejemplo típico es el cilindro de Tipler, un cilindro giratorio infinito. Y por supuesto, un clásico de la ciencia-ficción compatible con la relatividad general: los agujeros de gusano transitables (agujeros de Morris-Thorne).
Novikov & Hawking
Si las CTC (o en general, cualquier forma de viaje en el tiempo) fueran posibles, conllevarían peliagudas paradojas de difícil encaje con las leyes de la física. Los ejemplos más habituales en la literatura son la paradoja del abuelo (alterar el pasado de tal forma que el viaje que te llevó hacia él) y la paradoja bootstrap (una acción es causa de sí misma).
Para evitar estos efectos desagradables, Novikov estableció el principio de auto-consistencia, que dice que las únicas CTC posibles son aquellas que no incurren en paradojas. La justificación, al parecer, podría estar en el principio de mínima acción.
Hawking es aún más estricto con su conjetura de protección cronológica: según él, al incluir los efectos cuánticos a la relatividad general, las CTC serían imposibles. Sin una teoría unificada de la mecánica cuántica y la relatividad general es difícil saber si está en lo cierto, pero los cálculos en gravedad semiclásica (una aproximación a esta teoría unificada) lamentablemente parece que le dan la razón.
Querido lector, si eres un viajero en el tiempo, por favor indícame si estas teorías están en lo cierto. Y si es posible, ponte en contacto conmigo antes del 8 de septiembre de 2015.
Para saber más
Matt Viser: The quantum physics of chronology protection.
arXiv:gr-qc/0204022
Igor Novikov et al.: Time machines: the Principle of Self-Consistency as a consequence of the Principle of Minimal Action.
arXiv:gr-qc/9506087 y arXiv:gr-qc/9607063
Esta entrada está dedicada a mi hermana, Olga, que me sugirió la idea.
jueves, 3 de septiembre de 2015
Fondos cósmicos
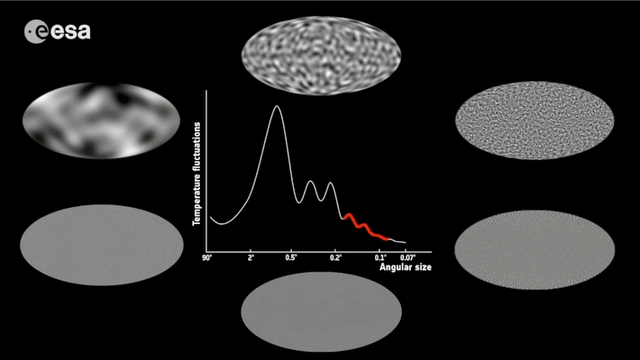
En las últimas décadas hemos aprendido un montón de cosas sobre la infancia del Universo. Las principales fuentes de información son la composición isotópica resultante de la nucleosíntesis del big bang y las fluctuaciones en la radiación cósmica de microondas (a la espera de una posible detección de ondas gravitatorias primordiales).
jueves, 27 de agosto de 2015
Resurgir de sus cenizas
Una vez más, Stephen Hawking vuelve a protagonizar todas las portadas en el mundillo de la física. Y es que ha anunciado que, junto con Strominger y Perry ha resuelto (el artículo aparecerá a finales de septiembre) uno de los "mayores" problemas que acechan a la física teórica: la información en los agujeros negros.
 |
| Visualización de un agujero negro, por Kip Thorne, para la película Interstellar |
sábado, 22 de agosto de 2015
La Qubit_era
Hoy en dia, hay problemas matemáticos que no son resolubles en los ordenadores "tradicionales". Hasta tal punto que la seguridad de nuestras comunicaciones por internet (incluyendo todas las transacciones bancarias) depende de esta incapacidad. El problema no está en que hagan falta procesadores más potentes. Son limitaciones de la arquitectura de un ordenador clásico. Para superarlas, necesitamos un nuevo tipo de ordenadores: los ordenadores cuánticos.
jueves, 13 de agosto de 2015
Una ración de helio
Para la entrada de hoy vamos a viajar un poco hacia atrás en el tiempo. Algo más de trecemil millones de años, concretamente. Eran tiempos interesantes, y aunque no los pudimos ver de primera mano, tenemos fuertes indicios de lo que "se cocía". Uno de ellos es la Nucleosíntesis del Big Bang (BBN). La formulación teórica se encuentra en el artículo "\(\alpha\beta \gamma \)" (Alpher-Bethe-Gamow). Antes de entrar en materia, la anécdota detrás de este artículo: la investigación la realizó el conocido físico ruso-americano George Gamow junto a su estudiante de doctorado Ralph Alpher. Pero Gamow era un graciosillo, y consideró que la lista de autores quedaría más redonda si completara el alfabeto griego invitando a Hans Bethe, físico nuclear y amigo personal de Gamow. Bethe no intervino en el articulo, pero curiosamente le tocó revisarlo para su publicación en Physical Review. A Alpher no le hizo ninguna gracia, porque pensaba que al compartir autoría con no uno sino dos de los mejores físicos del momento, se minusvaloraría su aportación. Posteriormente Bethe se interesaría por la nucleosíntesis, no la del Big Bang, sino la estelar, lo que le valdría el premio Nobel.
domingo, 9 de agosto de 2015
¿Sueñan los programas informáticos con ovejas eléctricas?
Los ordenadores han supuesto una verdadera revolución en numerosos aspectos de nuestra sociedad: desde la investigación en nuevos fármacos hasta el control del tráfico aéreo serían imposibles sin las capacidades de cálculo de estas maquinejas. Sin embargo, aún hay ciertos aspectos en los que los humanos ganamos a los ordenadores: uno de ellos es nuestra habilidad de aprender.
miércoles, 22 de julio de 2015
De chica en chica, y tiro porque me toca
No suelo ver mucho la tele, pero el otro día un anuncio me llamó la atención. Aparece un grupo de amigos en un coche (el cual se pretende anunciar), uno de ellos luciendo una escayola en el brazo. El grupo llega a la conclusión de que la fractura es culpa del karma, por la mala vida que llevaba el muchacho, en especial en lo relativo a las mujeres. Por lo tanto, debería compensar sus malas acciones visitando a todas las mujeres a las que ha hecho daño para pedirles perdón. El conductor muestra en la pantalla del coche una lista (bastante extensa) de afectadas. El de la escayola pregunta si tendrán suficiente gasolina para verlas a todas, a lo que el conductor responde, sin pensárselo ni un momento, con un sí muy rotundo. ¡Ese tío es un crack! - me refiero al conductor, no al de la escayola-.
martes, 21 de julio de 2015
Solución a la pregunta de la Ardilla de Oro 2015
El concurso de la Ardilla de Oro ya ha concluído, así que ya puedo contaros la respuesta a mi pregunta.
La ciudad de la pregunta era Königsberg, que era la capital de Prusia. En sus calles vivieron personajes de la talla de Kant, E. T. A. Hoffmann, Hilbert, Minkowski, Sommerfeld,...
Durante la Segunda Guerra Mundial, la ciudad de Königsberg sufrió importantes bombardeos, primero soviéticos y en 1944 de la RAF. El centro de la ciudad fue practicamente destruido, incluyendo la catedral y el castillo. En los últimos compases de la guerra, los soviéticos sitiaron y finalmente capturaron la ciudad. Tras la guerra, en la conferencia de Potsdam, se acordó que la ciudad y la región circundante quedaran bajo control soviético, concretamente de la República Rusa.
La ciudad fue reconstruída, y su nombre cambió a Kaliningrado. Tras la descomposición de la URSS, la región de Kaliningrado permaneció en Rusia. Sin embargo, está completamente rodeada por Polonia y Lituania, de modo que no existe una ruta por tierra que conecte Kaliningrado con el resto de Rusia. Esta situación se conoce como exclave en geografía, y como conjunto no conexo en topología.
Entre otras muchas razones, Königsberg es conocida por el problema de los siete puentes. Por la ciudad pasa el río Pregel (Pregolya), formando dos islas. En el siglo XVIII las distintas partes de la ciudad estaban unidas entre sí por siete puentes. La cuestión era si se podía dar un paseo en el que se cruzara cada uno de los puentes una sola vez. La fotografía en el post era de uno de estos puentes, el Holzbrück (puente de madera).
Leonard Euler propuso la solución en 1736, centrándose en las conexiones entre las distintas partes de la ciudad en vez de en las características geográficas (distancias, longitudes, ángulos,...). A continuación, Euler se dio cuenta de que en la región inicial y final debería de pasarse un número impar de veces, y en el resto de regiones un número par de veces. Como todas las regiones tenían un número impar de puentes, no era posible el camino buscado.
En el artículo en el que Euler propone su solución, hace una de las primeras referencias a lo que hoy se conoce como topología:
Además de la rama de la geometría que trata con distancias, y que siempre ha recibido toda la atención, hay otra rama, hasta ahora casi desconocida, a la que Leibnitz hizo la primera mención, llamándola geometría de la posición [geometriam situs]. Esta rama se ocupa únicamente de la determinación de la posición y sus propiedades; no involucra distancias ni cálculos hechos con ellas.
La interpretación actual de la solución de Euler se hace en términos de grafos, en los que las regiones de la ciudad se representan con nodos y los puentes con vértices. Sin embargo, Euler no utilizó este tipo de herramientas, y el primer uso registrado sucedió a principios del siglo XIX (Poinsot, 1810).
Actualmente en la ciudad de Kaliningrado hay ocho puentes (de los cuales cinco sobreviven desde tiempos de Euler), y es posible realizar un trayecto que visite cada uno de los puentes una sola vez.
Aprovecho la ocasión para felicitar al vencedor del concurso, José Luis "Pepelu" Bueno López, a todos los concursantes, a los anfitriones por el gran nivel de las preguntas, y por supuesto a Borja González Seoane y su blog por organizar esta actividad.
martes, 14 de julio de 2015
Vive rápido, muere joven y deja una bonita resonancia
La desintegración de alguna de las partículas elementales es uno de los procesos más rápidos que podemos observar. ¿Cómo podemos llegar a observar estas partículas tan efímeras, e incluso medir sus propiedades?
lunes, 13 de julio de 2015
Pregunta de la Ardilla de Oro 2015
El blog Metros por Segundo ha lanzado la iniciativa La Ardilla de Oro (#LaArdilladeOro) con el objetivo de promocionar la divulgación científica. La idea es ir saltando de blog en blog, cual ardilla en un bosque, respondiendo una serie de preguntas en el proceso. Desde Bosoneando hemos decidido unirnos en este evento. Si has seguido la ruta, procederás del blog Scire Science, y tu próximo destino será La Ciencia de la Vida. ¡Mucha suerte a todos los participantes!
Esta pregunta transcurre en una ciudad europea. Durante mucho tiempo
fue un importante centro cultural, que acogió a científicos, filósofos y
escritores. Sin embargo, durante un conflicto bélico fue prácticamente
destruida. Acabada la guerra, la ciudad pasó a otro de los estados
contendientes, y fue renombrada. Hoy en día la ciudad forma parte del
sucesor de aquel estado, aunque está separada del resto del territorio
por otros países (por lo que este estado no es conexo <-- ¡PISTA!).
Las calles de esta ciudad protagonizan un famoso enigma. Su solución la ideó un matemático helvético, y es considerada como el punto de inicio de una rama de las matemáticas. La pregunta es ¿cuál es el nombre de esta rama de las matemáticas? [La respuesta debe ser una única palabra]
sábado, 27 de junio de 2015
¿Materia oscura? Lávala con Axión
La identidad de la(s) partícula(s) que constituyen la materia oscura es, a día de hoy, un misterio. Lo único claro es que las partículas usuales del modelo estándar no son capaces de explicar las observaciones cosmológicas. Así que hay que buscar nuevos candidatos. Uno de los más prometedores es el axión.
Un problema muy fuerte
En física de partículas las simetrías son un elemento fundamental para construir las teorías. Tenemos simetrías gauge, simetrías de Lorentz y tres simetrías discretas: la reflexión espacial \(P\) (que cambia las coordenadas \(\vec{x}\) por \(-\vec{x}\)), la conjugación de carga \(C\) (que intercambia partículas y antipartículas) y la inversión temporal \(T\) (que cambia el sentido del tiempo).
En un inicio se pensaba que las teorías físicas respetaban las tres simetrías discretas. Sin embargo, los resultados experimentales de Wu mostraron que en las interacciones débiles se violaba la simetría \(P\). La siguiente hipótesis fue pensar que, aunque no se respetara la simetría \(P\), sí que se cumpliría la simetría \(CP\), es decir, cambiar partículas por antipartículas y darle la vuelta a las coordenadas. Pero de nuevo los experimentos dieron al traste con esta teoría, en este caso en la desintegración débil de los kaones (Nobel para Cronin y Fitch en 1980). Así que ahora tenemos que conformarnos con la simetría \(CPT\), que se tiene que cumplir para que no se viole la causalidad.
Una vez que la simetría \(CP\) perdió su estatus de pieza fundamental en la física de partículas, se investigó su papel en otras interacciones además de la débil. En concreto, se encontró que la interacción fuerte también admitía un término que violara la simetría \(CP\). Este término depende de un ángulo $\theta$. Pero los experimentos indican que las interacciones fuertes respetan la simetría \(CP\), lo que indica que \(\theta = 0\). A priori no hay ningún argumento que requiera que \(\theta=0\) en vez de cualquier otro valor, y el hecho de que así sea requiere un ajuste fino (fine tuning) de los parámetros. Esto es algo muy feo en física, y constituye lo que se conoce como problema CP fuerte.
Axión al rescate
La solución propuesta por Peccei y Quinn al problema CP fuerte fue el axión. En vez de ver \(\theta\) como un parámetro fijo, consideraron que era un campo \(\theta(x)\) con su propia dinámica, el campo axiónico. Para minimizar la energía, el valor de este campo era de manera natural \(\theta(x)=0\).
Los nombres que reciben las partículas son, en muchas ocasiones, bastante particulares: ya hemos visto partículas extrañas, con belleza (incluso belleza oculta), quarks, y puede que algún día hablemos de fantasmas y de pingüinos... El caso del axión no es una excepción. Uno de los padres del concepto, Frank Wilczek, se había quedado sin ideas de cómo llamar a este campo. Pero la inspiración le llegó en el momento más insospechado: mientras hacía la colada. El detergente que estaba usando era de la marca Axion, y el nombre le pareció llamativo, adecuado porque el nuevo campo "limpiaba" el problema, y además acababa en -on, como muchas de las pertículas ya conocidas.
Como en todo campo, hay una partícula asociada, el axión. El mecanismo de Peccei-Quinn requiere que el axión sea un bosón escalar (es decir, con espín 0) con masa muy pequeña y eléctricamente neutro.
El axión interacciona con la materia ordinaria de una manera muy débil: en un campo magnético muy intenso, un axión se puede transformar en un fotón, que sí se puede detectar.
Además, tras el big bang se habrían creado una gran cantidad de axiones, aun presentes hoy en día. Esto se debe a que en el universo primigenio el ángulo \(\theta(x)\) tomaba distintos valores en diversas regiones del universo, y durante su expansión \(\theta\) fue tendiendo a cero, creando excitaciones del campo, esto es axiones. Así que tenemos un gran número de partículas, que crean un campo gravitatorio pero por lo demás apenas se relacionan con las demás. Por ello se propone que los axiones puedan ser uno de los constituyentes de la materia oscura.
Telescopios de axiones
De momento, los axiones son solamente partículas hipotéticas. Sin embargo, hay varios experimentos diseñados para observarlos. Hace unos meses, el telescopio de rayos X XMM-Newton de la ESA reportó un exceso de rayos X que podría estar causado por la conversión de axiones en fotones en el campo magnético terrestre.
 |
| Variación temporal del flujo de rayos X procedentes de axiones detectado por XMM-Newton [fuente] |
De entre todos los experimentos que tratan de buscar axiones, unos de los más prometedores son los telescopios de axiones del CERN. Estos aparatos no buscan axiones que formen parte de la materia oscura, sino los que se producirían en el Sol. El experimento CAST, en marcha desde 2003, consta de un imán superconductor igual a los que se emplean en LHC y un detector de rayos X, que apuntan hacia el Sol durante el amanecer y el anochecer.
El CAST no ha encontrado señales de axiones en el rango de masas que es capaz de observar, por lo que ya está en marcha el diseño de su sucesor, el IAXO, que cuenta con imanes más potentes especialmente diseñados para esta misión. Tanto CAST como IAXO tienen una importante contribución española, de la Universidad de Zaragoza.
Para saber más
P. Berné: Aragón diseña un 'telescopio' para ver la materia oscura. Heraldo de Aragón, 27/672015
CAST Unizar group: CERN Solar Axion Telescope - CAST.
Enrique F. Borja: Materia oscura - toma uno - claqueta - axión. Cuentos cuánticos
Francisco R. Villatoro: La búsqueda de las axiones como candidatos a materia oscura. La ciencia de la mula Francis
viernes, 19 de junio de 2015
Estrellas de neutrones superconductoras
El universo es un lugar increíble. Hace poco he descubierto que un fenómeno tan exótico como la superconductividad se produce de forma natural en un ambiente tan extremo como una estrella de neutrones.
Estrellas de neutrones
Las estrellas de neutrones son, después de los agujeros negros, los objetos más densos del universo. Para empezar, una estrella de neutrones no es técnicamente una estrrella, ya que en su interior no se producen reacciones de fusión. Y aunque esté compuesta principalmente por neutrones, también contiene protones y algún que otro electrón.
Un objeto de tipo estelar es básicamente un equilibrio entre el colapso gravitatorio y algún tipo de presión que tiende a expandir el material. En las estrellas, esta presión viene de la radiación emitida en las reacciones nucleares. A medida que se agota el combustible para la fusión, la gravedad va dominando y la estrella se contrae y se hace más densa. Este proceso se detiene cuando los electrones no pueden estar más próximos entre sí debido al principio de exclusión de Pauli, lo que se conoce como presión de degeneración. Se ha formado una enana blanca.
Si la masa de la estrella inicial es elevada (al menos 10 veces la masa del Sol), la presión de degeneración de los electrones no es suficiente, y los electrones empiezan a combinarse con los protones para dar lugar a neutrones. Los neutrones detienen el colapso con su presión de degeneración. Este frenazo brusco causa una violenta explosión, una supernova tipo II, que expulsa la mayor parte del material estelar. Si el resto de supernova no supera las 5 masas solares, la presión de degeneración es suficiente para evitar futuros colapsos, y la estrella de neutrones resultante dedica el resto de su existencia a enfriarse tranquilamente.
 |
| Nebulosa del Cangrejo, restos de la supernova SN1054 con una estrella de neutrones en el centro. |
Tras la explosión, la estrella de neutrones conserva su momento angular, aunque su masa ha disminuido considerablemente. Por lo tanto, ahora rotará mucho más rápido. Esto significa que (más o menos) la estrella de neutrones actúa como una colosal dinamo, creando un campo magnético que puede llegar a \(10^{11}\)T (en la Tierra no se ha podido superar los 1000 T de manera controlada). Estas estrellas emiten radiación electromagnética que observamos de forma periódica (púlsar).
Cada oveja con su pareja
De lo grande pasamos a lo pequeño. La superconductividad es un estado de la materia en el que se produce conducción de la electricidad sin resistencia y expulsión del campo magnético. Teóricamente se explica mediante la teoría BCS (Bardeen, Cooper y Schrieffer). El aspecto más importante es que los electrones interaccionan entre sí (a través de la red cristalina) y forman parejas, los pares de Cooper, que se comportan como cuasipartículas. Estos pares tienen carácter bosónico, y por tanto no están sujetos al principio de exclusión de Pauli. Esto les permite a bajas temperaturas estar a todos los pares simultáneamente en el estado de mínima energía (condensado de Bose-Einstein), y así moverse sin impedimentos por el material.
La interacción que mantiene unidos a los electrones en un par de Cooper es extremadamente débil. Por ello, las altas temperaturas o campos magnéticos elevados dan al traste con la superconductividad. Actualmente los materiales conocidos con la superconductividad más resistente son cerámicas basadas en cupratos, con temperaturas críticas de hasta 133 K y campos críticos de 250 T.
Un fenómeno muy relacionado con la superconductividad es la superfluidez. Un superfluído es un líquido que no presenta viscosidad a bajas temperaturas debido al carácter bosónico de sus partículas (o pares de partículas, como en el helio-3). Un superfluído puede rebosar las paredes del recipiente que lo contiene.
Bardeen, Cooper y Schrieffer recibieron el Nobel en 1972 (Bardeen ha sido la única persona que ha recibido dos premios Nobel de física, el otro por la invención del transistor). Kapitsa recibió el Nobel en 1978 por el descubrimiento de la superfluidez del helio.
Super-estrellas
Una estrella de neutrones, al poco de su formación, puede tener temperaturas de hasta \(10^9\)K. ¿Cómo es posible, entonces, que sean superconductoras?
La respuesta es que los electrones no son las únicas partículas que pueden causar superconductividad. Debido a la extraordinaria densidad que hay en su interior, tanto los protones como los neutrones pueden formar pares, esta vez debido a la interacción fuerte. Esto significa que los neutrones son superfluídos, y los protones superfluídos y superconductores. La temperatura crítica es del orden de \(5\cdot10^8\)K, por lo que se puede decir que son los superconductores de más alta temperatura conocidos.
En la parte exterior del núcleo de la estrella, los protones forman un superconductor tipo II. Eso quiere decir que en el interior del superconductor hay unas regiones no superconductoras, llamadas vórtices, por donde escapa el flujo magnético. El campo magnético debido a esas regiones es inferior al campo crítico, pero aun así órdenes de magnitud superior a los que sabemos crear aquí en la Tierra. En las estrellas de neutrones con campos más extremos, los magnetares, puede llegar a \(10^{11}\)T. Esta hipótesis fue propuesta por Arkady Migdal en 1959.
La pregunta es obvia, ¿cómo hemos llegado a semejante conclusión? La respuesta es que observando cómo se enfrían las estrellas de neutrones. Se vio que algunas perdían calor muchísimo más rápido de lo que mostraban sus emisiones de rayos X. Se les echó la culpa (¡como siempre!) a los pobres neutrinos, que no los podemos ver fácilmente. Como el estado en el que dos protones o dos neutrones están apareados es energéticamente favorable, esta energía extra se libera en forma de neutrinos. Todo encaja.
Para saber más
D. Page et al.: Rapid Cooling of the Neutron Star in Cassiopeia A Triggered by Neutron Superfluidity in Dense Matter arXiv:1011.6142
P. S. Shternin et al.: Cooling neutron star in the Cassiopeia A supernova remnant: Evidence for superfluidity in the core arXiv:1012.0045
C. O. Heinke: Superfluids and superconductors in the core of a neutron star: the highest-temperature superconductor University of Alberta
B. Haskell et al.: Investigating superconductivity in neutron star interiors with glitch models arXiv:1209.6260
P. S. Shternin et al.: Cooling neutron star in the Cassiopeia A supernova remnant: Evidence for superfluidity in the core arXiv:1012.0045
C. O. Heinke: Superfluids and superconductors in the core of a neutron star: the highest-temperature superconductor University of Alberta
B. Haskell et al.: Investigating superconductivity in neutron star interiors with glitch models arXiv:1209.6260
sábado, 13 de junio de 2015
Otra vuelta de tuerca al espín
El espín es una propiedad fundamental de todas las partículas, y determina muchas de las propiedades de la materia, como la existencia de niveles electrónicos y enlaces químicos, y el magnetismo. Pero, ¿de dónde sale el espín?
miércoles, 10 de junio de 2015
Jugando en grupo: Lorentz y la venganza de los espinores
En una entrada anterior vimos que el grupo de Lorentz, que define las transformaciones legales en el juego de la relatividad especial, implicaban un cierto álgebra de Lie de sus generadores infinitesimales:
\[[J^k, J^l]=i \varepsilon_{klm}J^m \qquad [J^k, K^l]=i\varepsilon_{klm}K^m \qquad [K^k, K^l]=-i\varepsilon_{klm}J^m\]
Para hacer la notación un poco más compacta, podemos definir las matrices \(J^{\mu\nu}\) como
\[J^{23} = - J^{32} = J^1 \qquad J^{31}=-J^{13} =J^2 \qquad J^{12}=-J^{21}=J^3\]\[J^{01}=-J^{10} = K^1\qquad J^{02}=-J^{20} = K^2\qquad J^{03}=-J^{30}=K^3\]
y los parámetros de la transformación \(\omega_{\mu\nu}\) como \[\omega_{23} = - \omega_{32} = \theta^1 \qquad \omega_{31}=-\omega_{13} =\theta^2 \qquad \omega_{12}=-\omega_{21}=\theta^3\]\[-\omega_{01}=\omega_{10} = \eta^1\qquad -\omega_{02}=\omega_{20} = \eta^2\qquad -\omega_{03}=\omega_{30}=\eta^3\]
Con lo cual una transformación de Lorentz se puede reescribir como \[\Lambda = \exp\left(-\frac{i}{2}\omega_{\mu\nu}J^{\mu\nu}\right)\]y las relaciones de conmutación como
\[[J^{\mu\nu}, J^{\rho\sigma}] = i (g^{\nu\rho}J^{\mu\sigma} - g^{\nu\sigma}J^{\mu\rho} - g^{\mu\rho}J^{\nu\sigma} + g^{\mu\sigma} J^{\nu\rho}) \]
La matriz \(g^{\mu\nu}\) es la métrica del espacio. En la relatividad especial, es diagonal y tiene elementos \(\{1, -1, -1, -1\}\) (aunque también se puede elegir el convenio con los sognos opuestos)
La tarea que dejamos pendiente era encontrar representaciones para ese grupo, es decir, matrices que cumplieran las relaciones de conmutación. Vamos a ver unas cuantas:
Representación escalar
Es la opción más sencilla: no hacer nada. Si escogemos \(J^i = K^i = 0\), las relaciones de conmutación se cumplen, de un modo bastante evidente. Muchas cantidades físicas importantes trasnforman como escalares, como la masa, el intervalo espciotemporal, o la densidad lagrangiana.
Podemos ir un poco más allá y construir campos escalares, es decir, magnitudes cuyo valor dependa del punto (espaciotemporal), y que no cambien al hacer una transformación de Lorentz, \(\phi(x)\) \[\phi(x) \to \phi'(x') = \phi(x)\]
Adelantando un poco los acontecimientos, próximamente veremos que los campos están relacionados con las partículas. El mejor ejemplo de un campo escalar (complejo) es el archiconocido bosón de Higgs.
Representación vectorial
Si nuestro cometido es encontrar unas matrices con las mismas relaciones de conmutación que las \(J^i\), \(K^i\), una elección lógica es usar estas matrices. Así obtenemos la representación vectorial, en la que las matrices de la transformación son las \(\Lambda\) ya conocidas. Estas matrices tienen dimensión 4x4, por lo que actuaran sobre objetos de dimensión 4 a los que llamaremos cuadrivectores contravariantes. Cada una de las componentes las identificaremos con un superíndice \(x^\mu\). También etiquetaremos las filas de \(\Lambda\) con subíndices y las columnas con superíndices, y supondremos que se hace una suma en cada par de índices repetidos. Así, una transformación de Lorentz de un cuadrivector contravariante es \[x^\mu \to {x'}^\mu = {\Lambda^\mu}_\nu x^\nu\]
Otra representación sencilla consite en tomar \({J'}^i = J^i\), \({K'}^i = - K^i\), la representación conjugada. La matriz definida con estos generadores es \[{\Lambda_\mu}^\nu = \exp(-i\vec{\theta}\cdot\vec{J'} - i \vec{\eta}\cdot\vec{K'}) = g_{\rho\mu}{\Lambda^\rho}_\sigma g^{\sigma\nu}\]es la matriz hermítica a la de la representación vectorial. Ambas representaciones están relacionadas por una transformación de semejanza dada por \(g\), por lo que las representaciones vectorial y su conjugada son equivalentes. Los objetos de 4 componentes que transforman con esta representación se llaman cuadrivectores covariantes, y sus componentes se identifican mediante subíndices, \(x_\mu\):
\[x_\mu \to x'_\mu = {\Lambda_\mu}^\nu x_\nu\]
El producto de un vector covariante y otro contravariante es un escalar. Un ejemplo típico de cuadrivector es el cuadrimomento \(p^\mu = (E, \vec{p})\). Su módulo por tanto es un escalar, la masa:\[p^\mu p_\mu = g_{\mu\nu}p^\mu p^\nu = E^2 - p^2 = m^2\]
Si definimos un cuadrivector en cada punto del espaciotiempo, tenemos un campo vectorial \(A^\mu(x)\). En la física de partículas, los campos vectoriales son los encargados de mediar las interacciones: los fotones, los gluones y los bosones W y Z.
Representaciones tensoriales
En nuestros escarceos previos con la teoría de grupos, ya vimos que existía una receta para construir representaciones nuevas a partir de otras de dimensión menor: el producto tensorial. El grupo de Lorentz no es una excepción. Haciendo productos tensoriales de \(n\) vectores contravariantes y \(m\) vectores covariantes se obtiene un tensor de rango \((n,m\):\[V^{i_1}\otimes \cdots \otimes V^{i_n}\otimes V_{j_1}\otimes\cdots\otimes V_{j_m} = T^{i_1\cdots i_n}_{j_1\cdots j_m}\]
Para hacer su transformación de Lorentz, hay que incluir una \(\Lambda\) por cada índice. Por ejemplo, para un vector de rango 2:\[T^{\mu\nu} \to {T'}^{\mu\nu} = {\Lambda^\mu}_\rho {\Lambda^\nu}_\sigma T^{\rho\sigma}\]
Algunos tensores importantes son el tensor de energía-momento, la densidad de momento angular y, por supuesto, la métrica \(g\). Al pasar a campos tensoriales, tenemos el ejemplo del gravitón (de hecho, el gravitón es la métrica...).
Representación espinorial
¿Creíais que ya hemos visto todas las representaciones? Pues me temo que no, que el grupo de Lorentz aún nos depara una sorpresa. Para verlo, definimos las siguientes combinaciones de generadores:
\[A^i = J^i + i K^i \qquad B^i = J^i - i B^i\]Si las introducimos en el álgebra de Lie de Lorentz, encontramos las siguientes relaciones de conmutación:\[[A^i, A^j] = i\varepsilon_{ijk}A^k \qquad [B^i, B^j] = i\varepsilon_{ijk}B^k \qquad [A^i, B^j]=0\]¿Os suena de algo? Las matrices \(A\) y \(B\) definen dos álgebras de Lie de grupos SU(2) independientes. En jerga, esto se dice que el grupo de Lorentz es localmente isomorfo a SU(2)xSU(2). Por lo tanto, cada representación la podremos catalogar por el espín de cada uno de los generadores, \((j_1, j_2)\)
Como SU(2) ya lo conocemos bastante bien, podemos aprovecharlo para crear nuevas representaciones. Un ejemplo sencillo es tomar \(A^i = \sigma^i\) (las matrices de Pauli), y \(B^i = 0\), la representación (1/2, 0). La transformación es \[\Lambda_L = \exp\left[(-i\vec{\theta}-\vec{\eta})\cdot \vec{\sigma}\right]\]Esta transformaciones actúan sobre objetos con dos componentes, a los que llamaremos espinores de Weyl zurdos, \(\psi_L\).
Del mismo modo podemos construir la representación (0, 1/2) con los generadores \(A^i=0\), \(B^i = \sigma^i\). La transformación está dada (¡cuidado con el cambio de signo en la rapidez!) por \[\Lambda_R = \exp\left[(-i\vec{\theta}+\vec{\eta})\cdot \vec{\sigma}\right]\]Esta transformación actúa sobre los espinores de Weyl diestros \(\psi_R\).
Los espinores de Weyl están muy bien, aunque presentan algunos problemas: en primer lugar, al hacer una transformación de paridad, un espinor zurdo se transforma en diestro y viceversa. Además, cuando intentemos hacer partículas con espinores, estos no aceptan partículas masivas. Para solucionar ambos problemas, creamos los espinores de Dirac \(\psi_D\). Un espinor de Dirac tiene cuatro componentes, de las cuales las dos primeras transforman como un espinor de Weyl diestro y las otras dos como un espinor zurdo:
\[\psi_D = \begin{pmatrix} \psi_R\\\psi_L\end{pmatrix}\]
\[\psi_D \to \psi'_D = \begin{pmatrix} \Lambda_R & 0\\ 0 & \Lambda_L\end{pmatrix}\psi_D = \Lambda_D \psi_D\]
Los campos espinoriales representan a las partículas de "materia": electrones, quarks, neutrinos.
Suscribirse a:
Entradas (Atom)