Quarks de colorines

Murray Gell-Mann consiguió poner orden en el desconcierto que causaba la multitud de hadrones con la invención de tres partículas, los quarks, que constituirían todos los posibles mesones y bariones. Sin embargo, en un principio su idea no suscitó mucha adhesión, ya que proponía la existencia de unas partículas que no se habían visto nunca, y que además tenían carga eléctrica fraccionaria.

¿Cómo ver lo invisible?

Una primera pista de que los hadrones no son partículas elementales la ofrecen los momentos dipolares. El momento dipolar de una partícula con espín \(\vec{S}\) está dado por \[\vec{\mu} = g \frac{e}{2m}\vec{S}\]El factor-g determina el acoplamiento existente entre el momento angular y el campo magnético: si el momento angular es orbital, g=1 para las partículas cargadas y g=0 para las neutras. Si el momento se debe al espín, la ecuación de Dirac predice para una partícula cargada puntual g=2. La teoría cuántica de campos modifica ligeramente este valor por correcciones radiativas, elevándolo a g=2.0023. En el caso del electrón, el acuerdo con la teoría es espectacular (de hecho, es el valor teórico que reproduce con mayor precisión el valor experimental en toda la ciencia, con más de trece cifras significativas). Por el contrario, en el caso del protón y el neutrón falla estrepitosamente - notar que, aunque el neutrón sea neutro, su momento dipolar magnético no es nulo. Como la teoría nos ha dado tan buenos resultados con el electrón, no podemos simplemente tirarla. Lo lógico es pensar que han fallado las premisas iniciales: el protón y el neutrón no son puntuales.

El espaldarazo definitivo lo supuso el experimento de dispersión inelástica profunda realizado en SLAC. La idea es muy simple: siguiendo con el experimento de Hofstadter, se bombardea los hadrones [Nota técnica: los neutrones libres se desintegran rápidamente, por lo que en su lugar se utiliza deuterones, es decir, núcleos formados por un protón y un neutrón que sí son estables] con electrones muy energéticos, tanto que vamos a necesitar un acelerador de partículas. Con los resultados del experimento se puede inferir la distribución de carga eléctrica: en el protón tiene un máximo de carga en torno a 1/3 del radio, mientras que el neutrón tiene una zona de carga positiva en el interior, y de carga negativa en el exterior. Estos resultados son compatibles con un nucleón formado por tres cargas puntuales fraccionarias fuertemente ligadas, los tres quarks - técnicamente, tres quarks de valencia (es la tierra de las flores)-. Gell-Mann, padre de los quarks, se resistía a aceptar que tuvieran existencia real, a lo que se opuso firmemente Feynman, que defendía que los resultados experimentales apuntaban a que los hadrones están constituidos por partículas menores (a las que llamó partones en honor de Dolly Parton).

Y ahora, con tres nuevos sabores

En los años 60, se conocían dos generaciones de leptones (electrón-neutrino electrónico, muón-neutrino muónico), y "una y media" de quarks (up-down, strange). Glashow descubrió que un desiquilibrio entre el número de leptones y de quarks podía conllevar desastrosas consecuencias teóricas, por lo que propuso la existencia de un cuarto quark, encanto (charm, \(c\)), de carga +2/3.

Hubo que esperar hasta 1974 para poder encontrar el quark encantado. Sucedió en lo que se conoció como la Revolución de noviembre. Dos experimentos rivales, Fermilab y SLAC, encontraron sendas partículas, a las que bautizaron como \(J\) y \(\psi\), que resultaron tener la misma masa, carga, tiempo de desintegración y resto de propiedades. Habían descubierto simultáneamente lo que hoy conocemos como mesón \(J/\psi\). Además de la coincidencia del descubrimiento, este mesón con encanto (y no es un establecimiento hostelero) es singular por su largo tiempo de desintegración.

La explicación está en la regla OZI (por Okubu, Zweig e Iizuka), que explica en la desintegración de un mesón compuesto por un quark y su propio antiquark (quarkonio), los procesos conexos son mucho más probables que los inconexos. Un proceso conexo es aquél en el que los quarks de la partícula inicial siguen existiendo en las partículas finales; mientras que en un proceso inconexo los quarks del mesón se aniquilan entre sí, y con la energía liberada se crean nuevos quarks y antiquarks. En los mesones conocidos hasta entonces, el modo mayoritario de desintegración es el conexo, que tiene un tiempo de vida muy corto, mientras que los modos inconexos son menos frecuentes, y mucho más lentos.

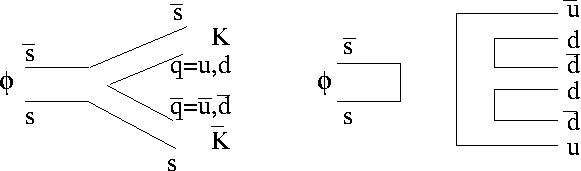Proceso conexo (izquierda) e inconexo (derecha)

En consecuencia, al encontrarse con un mesón que parecía que solo seguía modos inconexos, pero nunca los conexos, se interpretó como la evidencia del nuevo quark: Si no existían procesos conexos, significaba que no había ninguna combinación de hadrones más ligeros que el \(J/\psi\) y que contuvieran los quarks que lo forman. Pero si estos quarks eran los ya conocidos u, d, s, con la masa del \(J/\psi\) había numerosas posibilidades de procesos conexos. Con lo cual, cabe esperar que el revolucionario mesón estuviera formado por los quarks \(c\bar{c}\) (el resto de propiedades eran compatibles con esta hipótesis). Se produjeron más resonancias del \(J/\psi\) (partículas con la misma composición en quarks pero de mayor masa), que sí eran capaces de dar procesos conexos.

Ahora es necesario, para organizar los hadrones, usar el grupo SU(4), que añade como número cuántico el encanto, que es simplemente el contenido en quarks \(c\) del hadrón. Sin embargo, la masa del quark encanto, 1.5 GeV, es muy superior a la del resto, por lo que esta simetría es bastante inexacta.

Bariones con J=1/2 (izquierda) y J=3/2 (derecha)

Cuando parecía que el asunto entre el número de leptones y quarks parecía resuelto, salta la sorpresa. En SLAC, también durante la Revolución de noviembre, se descubre el leptón tau (al que va asociado un neutrino). Inmediatamente se proponen dos nuevos quarks, \(b\) y \(t\). Sus nombres en clave originales eran beauty y truth, pero desafortunadamente se impusieron los aburridos bottom y top. Para ampliar la simetría a SU(6) se necesitan otros dos números cuánticos más, bottomness y topness, que llevan la cuenta del número de quarks de cada tipo. Pero cada vez es más evidente que la simetría de sabor no existe: el quark bottom tiene una masa de 5 GeV, y la palma se la lleva el top, con nada más y nada menos que 175 GeV: es, con diferencia, la partícula elemental más masiva que conocemos, y pesa más que un átomo de oro.

Un toque de color

El modelo de quarks no estaba exento de problemas. El principal lo constituía la composición del hadrón \(\Omega^-\) que había previsto Gell-Mann (no era el único con problemas, al \(\Delta^{++}\) le ocurría lo mismo): Este barión tiene espín 3/2, carga -2 y extrañeza -3. Para poder reproducir estos números, el modelo postulaba que estaba compuesto por tres quarks \(s\) con el espín paralelo. ¡Pero eso es terrible! Los quarks son fermiones, por lo que el principio de exclusión de Pauli prohibe que tres de ellos compartan el mismo estado. Y sin embargo, parecía que los quarks lo estuvieran desobedeciendo.

La solución pasó, una vez más, por añadir números cuánticos que nos arreglen el desaguisado. Como ya habrás ido comprobando, los físicos de partículas tienen alma de poeta, y una imaginación infinita a la hora de poner nombres. El nuevo invento recibió el nombre de carga de color, y podía tomar tres valores, a saber, rojo, verde y azul. Los tres colores forman la representación fundamental del grupo SU(3) de color. A diferencia de lo que ocurre con el sabor, el color es una simetría exacta, y dos quarks que solo difieran en su color son completamente equivalentes.

Ahora tenemos más flexibilidad para construir los hadrones: en un barión, los tres quarks deben poseer carga de color neutra, lo cual se consigue teniendo uno de cada color. Para cumplir con la simetrización de la función de ondas, los hadrones son simétricos bajo el intercambio de partículas en la parte de sabor y espín, y antisimétricos en la parte de color \[\Omega^- = |sss\rangle |\uparrow\uparrow\uparrow\rangle |RGB + GBR + BRG - GRB - RBG - BGR\rangle\]Los mesones también tienen carga de color neutra, lo cual se consigue si el quark tiene un color, y el antiquark el anticolor correspondiente (los anticolores son los elementos de la representación conjugada del grupo de color).

¿Qué es lo que motiva a los hadrones a tener una carga de color neutra? Muy sencillo, que los quarks del mismo color se repelen y los de distinto color se atraen. Esta fuerza que une a los quarks es la fuerza fuerte en todo su esplendor (en realidad, lo que mantiene a protones y neutrones unidos en el núcleo son las sobras de esta fuerza, del mismo modo que algunas moléculas se unen por las sobras de la interacción electrostática en su interior, fenómeno conocido como fuerzas de van der Waals), y la rama de la física que la estudia es la cromodinámica cuántica (QCD para los amigos). El origen de esta fuerza se puede explicar, como ya ocurriera con el electromagnetismo, mediante una teoría gauge: al promocionar la simetría de color a simetría local, aparecen nuevos campos que actúan como mediadores de la fuerza. En el caso de la QCD, estos mediadores son los elementos de la repr 8 resultante al combinar \(\mathbb{3}\otimes\mathbb{3}^\star\), y se conocen como gluones.

Hasta que la QCD nos separe

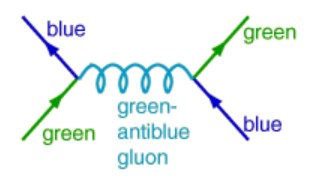
Los ocho gluones son partículas sin masa ni carga eléctrica, y con espín 1. Pero su principal peculiaridad es que tienen un color y un anticolor, por lo que presentan carga de color neta. La interacción entre dos quarks se realiza al cambiar estos de color, mediante el intercambio de un gluón que transporta los colores intercambiados, respetando en todo momento la conservación del color.

Hasta aquí, todo va bien. Lo interesante es que, como los gluones tienen carga de color, pueden interaccionar con otros gluones. Esto significa que un gluón puede descomponerse en dos gluones con la misma carga: al contrario de lo que ocurre en la electrodinámica, la carga de color se refuerza, se antiapantalla al aumentar la distancia.

Esto da lugar a dos curiosos fenómenos característicos de la cromodinámica: cuando dos quarks están muy próximos, la fuerza entre ellos es realmente pequeña, y se comportan como partículas libres (libertad asintótica). Pero si intentamos separar los dos quarks, la energía que los une aumenta descontroladamente, hasta que es suficiente para crear un par quark-antiquark que alivie la tensión: por ello, es imposible conseguir aislar un quark individual (confinamiento de color).

El confinamiento presenta formidables retos: desde el punto de vista experimental, las energías puestas en juego en los colisionadores de partículas son capaces de, partiendo un único barión, producir cientos de partículas hadrónicas, lo que se conoce como jet, que complica mucho la identificación de los procesos. Y desde el punto de vista teórico, el enfoque actual de la teoría cuántica de campos es perturbativo: se empieza con los términos que contengan menos partículas virtuales, y en las sucesivas aproximaciones se van incluyendo más nodos de interacción. Como en la cromodinámica los términos en los que intervienen más gluones son los más energéticos, este enfoque no se puede emplear: la QCD no es perturbativa.

Para saber más

Enrique F. Borja: Extrañas estrellas extrañas, ¿Coloreamos?, Rómpelo y dime qué hay dentro... Cuentos Cuánticos
Flip Tanedo: Meet the quarks, World of glue, QCD and confinement. Quantum Diaries.