Los sistemas de unidades son muy prácticos para determinados cálculos. Sin embargo, el valor numérico de las magnitudes dimensionales no es algo fundamental, ya que depende del sistema de unidades elegido. Por el contrario, las magnitudes adimensionales son iguales en todas las unidades posibles. Al igual que las constantes matemáticas como \(\pi\) o \(e\), las constantes físicas adimensionales son las que nos proporcionan información sobre el funcionamiento del universo. Pero guardan una diferencia respecto de las constantes matemáticas: no pueden ser calculadas, sino que debemos determinarlas experimentalmente.
Hay diversas formas de definir la constante de estructura fina, siempre como el cociente de dos magnitudes con dimensiones. Una posibilidad es usar la relación entre la velocidad de una partícula cargada en un sistema electromagnéticamente ligado (véase átomo de hidrógeno) con la velocidad de la luz \(v = \alpha c\). Podríamos resolver el átomo de hidrógeno con la ecuación de Schrödinger, pero afortunadamente Bohr, años antes del descubrimiento de esta ecuación, consiguió resolverlo con unas cuantas suposiciones ad hoc: En primer lugar, la cuantización del momento angular \(L = m \hbar\). Aquí solo consideraremos el primer nivel, por lo que \(L = a_0 m_e v = \hbar\). El otro punto de su teoría es que la fuerza electrostática actúa como fuerza centrípeta \[\frac{e^2}{4\pi\varepsilon_0 {a_0}^2} = \frac{m_e v^2}{a_0}\] Eliminando el radio de Bohr de ambas ecuaciones \[a_0 = \frac{e^2}{4\pi\varepsilon_0 m_e v^2} = \frac{\hbar}{m_e v}\]
Por lo que la velocidad es \[v = \frac{e^2}{4\pi\varepsilon_0 \hbar} = \alpha c\] y finalmente obtenemos la constante de estructura fina en términos de constantes universales con dimensiones:
\[\alpha = \frac{e^2}{4\pi \varepsilon_0 \hbar c}\]
Los niveles de energía en el átomo de hidrógeno (no relativista) se pueden expresar de forma sencilla con nuestra querida constante: \[E_n = \frac{-1}{n} \alpha^2\frac{1}{2}mc^2\]
La constante de estructura fina también relaciona tres importantes escalas de longitud del electrón: el radio de Bohr \(a_0\), la longitud de onda Compton \(\lambda_e\) (donde hay que empezar a considerar los efectos relativistas, como la creación de pares de partícula-antipartícula) y el radio clásico del electrón \(r_e\) (donde la interacción del electrón con su propio campo electromagnético empieza a causar problemas):\[r_e = \alpha \lambda_e = \alpha^2 a_0\]
A todo esto, aún no hemos contado cuál es el origen del nombre de esta constante. Ni el modelo de Bohr ni la ecuación de Schrödinger con potencial coulombiano tienen en cuenta los efectos relativistas. Poco después de la aparición del modelo de Bohr, Sommerfeld lo modificó para suplir esta deficiencia. Como solución encontró que los niveles de Bohr se desdoblaban en subniveles muy próximos, lo que los espectroscopistas ya habían observado y catalogado como "estructura fina" (en contraposición a la estructura gruesa que eran los niveles). La separación de estas líneas, para el nivel \(n\), es del orden de \(\alpha^2 E_n\).
Años más tarde, la teoría cuántica siguió avanzando, y a Bohr le sucedieron Schrödinger, y después Dirac. Aplicando la ecuación de Schrödinger tal cual, solo con el potencial de Coulomb, no es posible obtener la estructura fina. Sin embargo, si se toman de la ecuación de Dirac los ingredientes necesarios (correcciones relativistas a la energía cinética, interacción del espín del electrón con el campo magnético y el término de Darwin - nieto - que da cuenta de la no-localidad del electrón debida al Zitterbewegung) y se añaden a mano como correcciones, sí que se obtiene el resultado esperado. Con la técnica empleada para introducir las correcciones, la teoría de perturbaciones, se realiza el desarrollo en serie de potencias de un término que parametriza la intensidad de la perturbación, y en este caso es nuestra querida \(\alpha\).\[E_n = \frac{mc^2}{\left[ 1+ \frac{\alpha^2}{\left(n-j-1/2 + \sqrt{(j+1/2)^2 - \alpha^2} \right)^2}\right]^{1/2}}\approx mc^2 \left[ 1 - \frac{1}{2}\frac{\alpha^2}{n^2} + \frac{1}{2}\frac{\alpha^4}{n^3}\left(\frac{1}{j+1/2} - \frac{3}{4n}\right)\right]\]
En las integrales, cada línea interna contribuye con un propagador (la probabilidad de que la partícula pase de un punto a otro del espacio), y cada vértice con un factor \(g\), que es la intensidad de la interacción entre las partículas. En el caso del electromagnetismo, esta constante de acoplamiento es precisamente la constante de estructura fina \(g = \sqrt{\alpha}\).
Podemos clasificar los diagramas según el número de vértices que tengan. Para un diagrama con \(n\) vértices, su probabilidad irá como \(|\mathcal{M_n}|^2\sim \alpha^n\). Como en el caso del electromagnetismo \(\alpha \ll 1\), eso significa que los diagramas con dos vértices son más probables que los de cuatro vértices, que a su vez son más probables que los de seis.... Esto permite que, en la práctica, no sea necesario calcular los -infinitos- diagramas, sino que se pueda parar a unos pocos órdenes: el electromagnetismo es tratable mediante técnicas perturbativas.
El hecho de que en la electrodinámica cuántica haya que tener en cuenta todos los diagramas de Feynman nos hace otra jugarreta: la constante de estructura fina ni siquiera es constante, sino que depende de la energía.
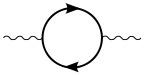
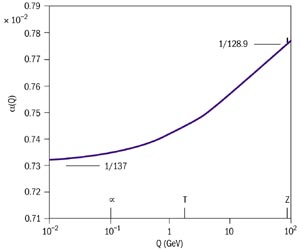
Este hecho está íntimamente ligado a la estructura del vacío: y es que el vacío no significa ausencia de partículas, sino que es simplemente el estado de mínima energía posible. En el vacío se están continuamente creando y aniquilando parejas de partícula-antipartícula virtuales, correspondientes a los diagramas de Feynman en los que un fotón da lugar a un bucle. Dado que las dos partículas virtuales (normalmente electrón y positrón) tienen carga eléctrica, se verán afectadas si hay algún electrón real por allí cerca, y se orientarán como un dipolo eléctrico (polarización del vacío). Por lo tanto, si observamos el electrón desde grandes distancias (equivalentemente, a bajas energías), en realidad estamos viendo un electrón real con su séquito de acompañantes virtuales, que apantallan su carga: la carga observada es menor que la real. A medida que sondeamos más cerca (distancias menores que \(r_e\)), a mayores energías, podemos ir deshaciéndonos de las molestas partículas virtuales y conocer al electrón en toda su intimidad (como ves, el electrón no es tan diferente de los humanos. Pero eso está más allá del alcance de esta entrada...) y ver su carga sin apantallar, por lo que será mayor de la que conocemos en el límite de bajas energías. Así pues, el valor de la constante de estructura fina depende de la energía - se dice que "corre" con la energía - y la técnica matemática para describirlo se conoce como renormalización. De hecho, los resultados experimentales indican que, a energías de 90 GeV, \(\alpha^{-1} \approx 128\).
Enrique F. Borja: Cuántica y garabatos. Cuentos cuánticos
Franz Muheim: Quantum electrodynamics. University of Edinburgh
CERN Courier: Fifty years of the renormalization group
Esta entrada participa en la LIX edición del carnaval de Física organizada por El mundo de las ideas, cuyo título es ¿Cuál es tu constante o variable favorita?
Más física en mi cuenta de twitter @bosoneando, o en google +
Probablemente la constante adimensional más popular en física es la constante de estructura fina \(\alpha\). Esta constante da cuenta de la intensidad de la fuerza electromagnética, y su valor es \[\alpha = 7.297\,352\,5698\,\cdot\,10^{-3}= \frac{1}{137.035\,999\,074}\]
El hecho de que su inverso fuera prácticamente un número entero suscitó interpretaciones numerológicas, incluso de gente seria como Eddington o Dirac. Sin llegar a tales extremos, Feynman sí que declaró su fascinación por el numerito:
"Hay una cuestión muy profunda y bella asociada con la constante de acoplamiento \(e\) observada - la amplitud de un electrón real para emitir o absorber un fotón real. Es un número sencillo que ha sido determinado experimentalmente a cerca de 0.08542455. (Mis amigos físicos no reconocerán este número, porque les gusta recordar el inverso de su cuadrado: 137.03587 con una incertidumbre de aproximadamente 2 en la última cifra decimal [1]. Ha sido un misterio incluso desde su descubrimiento hace más de cincuenta años, y todos los buenos físicos teóricos han puesto este número en sus paredes y se han preocupado por él). Inmediatamente querrás saber de dónde viene este número para el acoplamiento: ¿está relacionado con pi o quizás con la base de los logaritmos naturales? Nadie lo sabe. Es uno de los malditos grandes misterios de la física: un número mágico que viene a nosotros sin conocimiento humano. Puedes decir que 'la mano de Dios' [2] escribió ese número y que 'no sabemos cómo movió su lápiz'. Sabemos qué tipo de baile hay que hacer para medir experimentalmente ese número con gran precisión, ¡pero no qué baile hay que hacer en el ordenador para sacar este número sin haberlo metido antes secretamente!" - Richard P. Feynman, QED: The strange theory of light and matter. 1985
[1]: Valores de 1985
[2]: No entiendo qué tiene que ver Maradona en todo esto
[1]: Valores de 1985
[2]: No entiendo qué tiene que ver Maradona en todo esto
Hay diversas formas de definir la constante de estructura fina, siempre como el cociente de dos magnitudes con dimensiones. Una posibilidad es usar la relación entre la velocidad de una partícula cargada en un sistema electromagnéticamente ligado (véase átomo de hidrógeno) con la velocidad de la luz \(v = \alpha c\). Podríamos resolver el átomo de hidrógeno con la ecuación de Schrödinger, pero afortunadamente Bohr, años antes del descubrimiento de esta ecuación, consiguió resolverlo con unas cuantas suposiciones ad hoc: En primer lugar, la cuantización del momento angular \(L = m \hbar\). Aquí solo consideraremos el primer nivel, por lo que \(L = a_0 m_e v = \hbar\). El otro punto de su teoría es que la fuerza electrostática actúa como fuerza centrípeta \[\frac{e^2}{4\pi\varepsilon_0 {a_0}^2} = \frac{m_e v^2}{a_0}\] Eliminando el radio de Bohr de ambas ecuaciones \[a_0 = \frac{e^2}{4\pi\varepsilon_0 m_e v^2} = \frac{\hbar}{m_e v}\]
Por lo que la velocidad es \[v = \frac{e^2}{4\pi\varepsilon_0 \hbar} = \alpha c\] y finalmente obtenemos la constante de estructura fina en términos de constantes universales con dimensiones:
\[\alpha = \frac{e^2}{4\pi \varepsilon_0 \hbar c}\]
Los niveles de energía en el átomo de hidrógeno (no relativista) se pueden expresar de forma sencilla con nuestra querida constante: \[E_n = \frac{-1}{n} \alpha^2\frac{1}{2}mc^2\]
La constante de estructura fina también relaciona tres importantes escalas de longitud del electrón: el radio de Bohr \(a_0\), la longitud de onda Compton \(\lambda_e\) (donde hay que empezar a considerar los efectos relativistas, como la creación de pares de partícula-antipartícula) y el radio clásico del electrón \(r_e\) (donde la interacción del electrón con su propio campo electromagnético empieza a causar problemas):\[r_e = \alpha \lambda_e = \alpha^2 a_0\]
La estructura fina
 |
| Espectro del sodio. Si amplias la imagen verás que la línea amarilla (580 nm) en realidad son dos líneas muy próximas (doblete amarillo del sodio). El desdoblamiento se debe a la estructura fina. |
A todo esto, aún no hemos contado cuál es el origen del nombre de esta constante. Ni el modelo de Bohr ni la ecuación de Schrödinger con potencial coulombiano tienen en cuenta los efectos relativistas. Poco después de la aparición del modelo de Bohr, Sommerfeld lo modificó para suplir esta deficiencia. Como solución encontró que los niveles de Bohr se desdoblaban en subniveles muy próximos, lo que los espectroscopistas ya habían observado y catalogado como "estructura fina" (en contraposición a la estructura gruesa que eran los niveles). La separación de estas líneas, para el nivel \(n\), es del orden de \(\alpha^2 E_n\).
Años más tarde, la teoría cuántica siguió avanzando, y a Bohr le sucedieron Schrödinger, y después Dirac. Aplicando la ecuación de Schrödinger tal cual, solo con el potencial de Coulomb, no es posible obtener la estructura fina. Sin embargo, si se toman de la ecuación de Dirac los ingredientes necesarios (correcciones relativistas a la energía cinética, interacción del espín del electrón con el campo magnético y el término de Darwin - nieto - que da cuenta de la no-localidad del electrón debida al Zitterbewegung) y se añaden a mano como correcciones, sí que se obtiene el resultado esperado. Con la técnica empleada para introducir las correcciones, la teoría de perturbaciones, se realiza el desarrollo en serie de potencias de un término que parametriza la intensidad de la perturbación, y en este caso es nuestra querida \(\alpha\).\[E_n = \frac{mc^2}{\left[ 1+ \frac{\alpha^2}{\left(n-j-1/2 + \sqrt{(j+1/2)^2 - \alpha^2} \right)^2}\right]^{1/2}}\approx mc^2 \left[ 1 - \frac{1}{2}\frac{\alpha^2}{n^2} + \frac{1}{2}\frac{\alpha^4}{n^3}\left(\frac{1}{j+1/2} - \frac{3}{4n}\right)\right]\]
La constante de estructura fina en los diagramas de Feynman
Posiblemente hayas visto alguna vez un diagrama de Feynman. Esos dibujitos en los que se ven a partículas entrando y saliendo, pasando por estados intermedios. Pues que sepas que, en realidad, todo es un engaño. Los diagramas de Feynman no son más que una forma muy compacta (y muy vistosa) de escribir una integral, cuyo resultado \(\mathcal{M}\) (su módulo al cuadrado \(|\mathcal{M}|^2\)) da la probabilidad del proceso representado por las líneas externas de las partículas iniciales y finales siguiendo un determinado mecanismo de reacción (representado por las líneas internas). Para obtener la probabilidad total de que a partir de las partículas iniciales se obtengan las finales, hay que sumar los numeritos procedentes de todos los diagramas posibles (que cumplan las leyes de conservación) que se puedan dibujar con esas mismas líneas externas. Y con todos, quiero decir todos, infinitos.En las integrales, cada línea interna contribuye con un propagador (la probabilidad de que la partícula pase de un punto a otro del espacio), y cada vértice con un factor \(g\), que es la intensidad de la interacción entre las partículas. En el caso del electromagnetismo, esta constante de acoplamiento es precisamente la constante de estructura fina \(g = \sqrt{\alpha}\).
Podemos clasificar los diagramas según el número de vértices que tengan. Para un diagrama con \(n\) vértices, su probabilidad irá como \(|\mathcal{M_n}|^2\sim \alpha^n\). Como en el caso del electromagnetismo \(\alpha \ll 1\), eso significa que los diagramas con dos vértices son más probables que los de cuatro vértices, que a su vez son más probables que los de seis.... Esto permite que, en la práctica, no sea necesario calcular los -infinitos- diagramas, sino que se pueda parar a unos pocos órdenes: el electromagnetismo es tratable mediante técnicas perturbativas.
Cuando las constantes corren
El hecho de que en la electrodinámica cuántica haya que tener en cuenta todos los diagramas de Feynman nos hace otra jugarreta: la constante de estructura fina ni siquiera es constante, sino que depende de la energía.
Este hecho está íntimamente ligado a la estructura del vacío: y es que el vacío no significa ausencia de partículas, sino que es simplemente el estado de mínima energía posible. En el vacío se están continuamente creando y aniquilando parejas de partícula-antipartícula virtuales, correspondientes a los diagramas de Feynman en los que un fotón da lugar a un bucle. Dado que las dos partículas virtuales (normalmente electrón y positrón) tienen carga eléctrica, se verán afectadas si hay algún electrón real por allí cerca, y se orientarán como un dipolo eléctrico (polarización del vacío). Por lo tanto, si observamos el electrón desde grandes distancias (equivalentemente, a bajas energías), en realidad estamos viendo un electrón real con su séquito de acompañantes virtuales, que apantallan su carga: la carga observada es menor que la real. A medida que sondeamos más cerca (distancias menores que \(r_e\)), a mayores energías, podemos ir deshaciéndonos de las molestas partículas virtuales y conocer al electrón en toda su intimidad (como ves, el electrón no es tan diferente de los humanos. Pero eso está más allá del alcance de esta entrada...) y ver su carga sin apantallar, por lo que será mayor de la que conocemos en el límite de bajas energías. Así pues, el valor de la constante de estructura fina depende de la energía - se dice que "corre" con la energía - y la técnica matemática para describirlo se conoce como renormalización. De hecho, los resultados experimentales indican que, a energías de 90 GeV, \(\alpha^{-1} \approx 128\).
Para saber más...
John Baez: Length scales in physicsEnrique F. Borja: Cuántica y garabatos. Cuentos cuánticos
Franz Muheim: Quantum electrodynamics. University of Edinburgh
CERN Courier: Fifty years of the renormalization group
Esta entrada participa en la LIX edición del carnaval de Física organizada por El mundo de las ideas, cuyo título es ¿Cuál es tu constante o variable favorita?
Más física en mi cuenta de twitter @bosoneando, o en google +




no he entendido nada.parece el lenguaje de una logia secreta. jeje.
ResponderEliminarcool
ResponderEliminarEl lenguaje de Dios y el universo....los números. Excelente, gracias!!!
ResponderEliminar