Voy a correr el riesgo de parecer pesao, pero voy a volver a hablar de lo supergeniales que son las simetrías. Las simetrías hacen nuestra descripción del mundo más sencilla, más eficiente, más elegante. Además, también nos permiten predecir algunas propiedades de los sistemas físicos, como la existencia de magnitudes conservadas (¡gracias, Emmy!) o las secciones eficaces de distintos procesos.
Tras esta cuña publicitaria, vamos a hablar de una simetría muy común en la vida cotidiana, así como en la física: la rotación.
Una rotación es una transformación de un vector en otro con el mismo módulo, pero distinta dirección, y dejando invariante el origen. Si nos restringimos a un plano, la rotación de un vector \(\vec{r} = (x, y)\) se puede escribir como \[x' = x \cos\theta + y \sin\theta \qquad \qquad y' = y \cos \theta - x \sin\theta\] que en forma de matriz queda\[\begin{pmatrix} x'\\y'\end{pmatrix} = \begin{pmatrix} \cos \theta & \sin \theta \\ -\sin\theta & \cos \theta \end{pmatrix}\begin{pmatrix} x \\ y\end{pmatrix}\]La matriz de rotación se caracteriza por ser ortonormal (esto es, unitaria pero con todos los elementos reales) y con determinante + 1. Las matrices ortogonales de dimensión \(N\) forman el grupo ortogonal \(\mathrm{O}(N)\), y con la condición sobre el determinante, el grupo ortonormal \(\mathrm{SO}(N)\). Por lo tanto, las rotaciones en el plano forman el grupo SO(2).
Ahora pasemos a tres dimensiones. Las rotaciones siguen conservando las magnitudes de los vectores, por lo que formarán el grupo SO(3). Para describir una rotación en 3d hacen falta tres parámetros. Hay diferentes elecciones, pero una de las más claras es la de un eje de giro \(\hat{n} = (n_x, x_y, n_z)\) (dado que es un vector de módulo 1, realmente solo son dos parámetros) y un ángulo \(\theta\). Con ellos, la rotación se puede escribir como \[R(\theta, \hat{n}) = I + \sin\theta \begin{pmatrix}0 & -n_z & n_y\\ n_z & 0 & -n_x \\ -n_y & n_x & 0 \end{pmatrix}+ (\cos\theta-1)\begin{pmatrix}0 & -n_z & n_y\\ n_z & 0 & -n_x \\ -n_y & n_x & 0 \end{pmatrix}^2\]
A continuación vamos a probar a hacer una rotación infinitesimalmente pequeña, de ángulo \(\epsilon\) tal que \(\sin\epsilon \approx \epsilon\) y \(\cos\epsilon \approx 1\):\[R(\epsilon, \hat{n}) \approx I + \epsilon \begin{pmatrix}0 & -n_z & n_y\\ n_z & 0 & -n_x \\ -n_y & n_x & 0 \end{pmatrix}\]
Como ya vimos, esto nos permite definir los generadores infinitesimales del grupo \[R = I - i(\hat{n}\cdot\vec{L}) \epsilon\]\[L_x = \begin{pmatrix}0 & 0 & 0\\ 0 & 0 & -i \\ 0 & i & 0\end{pmatrix} \qquad L_y = \begin{pmatrix} 0 & 0 & i\\ 0 & 0 & 0 \\-i & 0 &0 \end{pmatrix} \qquad L_z = \begin{pmatrix} 0 & -i & 0\\i & 0 & 0\\ 0 & 0 & 0\end{pmatrix}\] Integrando al ángulo de giro se obtiene que \[R(\theta, \hat{n}) = \exp[i(\hat{n}\cdot\vec{L}) \epsilon] = I + \sum_{j=1}^\infty \frac{i^j\theta^j}{j!}(\hat{n}\cdot\vec{L})^j\]
Como los generadores infinitesimales cumplen la curiosa propiedad \((\hat{n}\cdot\vec{L})^3 = (\hat{n}\cdot\vec{L})\), esto se convierte en \[R(\theta, \hat{n}) = I + i (\hat{n}\cdot\vec{L})\sum_{k=0}^\infty\frac{(-1)^k \theta^{2k+1}}{(2k+1)!} + (\hat{n}\cdot\vec{L})^2\sum_{k=1}^\infty \frac{(-1)^k \theta^{2k}}{(2k)!} = \]\[= I+ (\hat{n}\cdot\vec{L})\sin\theta + (\hat{n}\cdot\vec{L})^2 (1-\cos\theta)\]
Esta es la expresión de la que partíamos, así que hemos hecho un giro de \(2\pi\) (muy oportuno para esta entrada). En el camino, hemos visto los generadores del grupo, y la expresión de la rotación como una exponencial. Con esta expresión hay que tener cuidado, ya que las exponenciales de matrices pueden ser traicioneras\[\exp(i \theta \hat{n}\cdot\vec{L}) = \exp[i\theta(n_xL_x + n_yL_y + n_z Lz)]\neq \exp(i\theta n_xL_x)\exp(i\theta n_y L_y)\exp(i\theta n_z L_z)\]
La exponencial de una suma de matrices está dada por la fórmula de Zassenhaus \(\exp(A+B) = \exp A \exp B \exp(-[A, B]/2) \cdots\) (a continuación vienen más conmutadores anidados). Lo que me recuerda que aún no hemos calculado el álgebra de Lie correspondiente al grupo:
\[[L_x, L_y] = i L_z \qquad [L_y, L_z]=iL_x \qquad [L_z, L_x]=iL_y\]
¿Os suena de algo? Es igual que el álgebra de Lie de SU(2), con las matrices \(\frac{1}{2}\vec{\sigma}\) -¡dichoso \(\frac{1}{2}\)-. Y allí dijimos que el álgebra de Lie determina por completo el grupo. Lo que ocurre es que determina su comportamiento para parámetros pequeños, pero no para cualquier valor: ¿Qué ocurre al hacer una "rotación" de \(2\pi\), \(\exp(i2\pi\hat{n}\cdot\frac{1}{2}\vec{\sigma})\) usando una matriz de SU(2)? Pues depende de la representación en la que nos encontremos: si es de dimensión impar \[\exp i2\pi \frac{1}{2}\sigma_z^{(3)} = \exp \begin{pmatrix} i2\pi & 0 & 0\\ 0 & 0 & 0 \\ 0 & 0 & -i2\pi\end{pmatrix} = \begin{pmatrix} e^{i2\pi} & 0 & 0\\ 0 & e^0 & 0 \\ 0 & 0 & e^{-i2\pi}\end{pmatrix} = I \]De momento, todo bien. Pero, al hacer lo mismo con las representaciones de dimensión par...\[\exp i2\pi \frac{1}{2}\sigma_z = \exp\begin{pmatrix}i\pi & 0\\ 0 & -i\pi\end{pmatrix} = \begin{pmatrix}e^{i\pi} & 0 \\ 0 & e^{-i\pi}\end{pmatrix} = -I\] Así que, para conseguir volver a la posición inicial, haría falta un giro de ¡\(4\pi\)! [Técnicamente, SU(2) es el recubrimiento doble de SO(3)]
En consecuencia, si queremos hacer la representación de una rotación en un espacio vectorial complejo, deberemos tomar una dimensión impar. Y las representaciones de dimensión par las vamos a dejar en el banquillo (de momento ;))
Vamos a intentar dar respuesta a las dos primeras cuestiones (la tercera la tendrás que descubrir tú). Y como lo cuántico siempre es mejor -ahora que lo pienso, ese hubiera sido un buen lema para el blog - vamos a rotar las funciones de onda. Como estamos en un espacio complejo, es obvio que necesitaremos las representaciones -de dimensión impar- del buen SU(2).
Pero antes, a la cantidad conservada. Unos conocimientos a nivel usuario de la mecánica clásica son suficientes para haberse topado con el momento angular \[\vec{J} = \vec{r}\times\vec{p} = (yp_z - zp_y, zp_x - x p_z, x p_y - y p_x)\]
Para obtener su versión cuántica, no hay más que sustituir las posiciones y momentos por sus respectivos operadores \(\vec{J} = \vec{R}\times\vec{P}\). Vamos a ver qué ocurre con los conmutadores de las diferentes componentes del momento angular:
\[[J_x, J_y] = [Y P_z - Z P_y, Z P_x - X P_z] =\]\[ [Y P_z, Z P_x]+ [Y P_z, -X P_z]+ [-Z P_y, Z P_x] + [-Z P_y, -X P_z]=\]\[= YZ[P_z, P_x] + Y[P_z, Z]P_x+Z[Y, P_x]P_z+ [Y, Z]P_x P_z-\]\[ - XY[P_z, P_z] - Y[P_z, X]P_z - X[Y, P_z]P_z - [Y,X]P_zP_z\]\[-ZZ[P_y, P_x] - Z[P_y, Z]P_x - Z[Z, P_x]-[Z,Z]P_yP_x+\]\[+XZ[P_y, Pz]+Z[P_y, X]P_z + X[Z, P_z]P_y + [Z, X]P_yP_z=\]\[= Y[P_z, Z]P_x + X[Z, P_z]P_y = i\hbar(X P_y - Y P_x) = i\hbar J_z\]
Del mismo modo también se cumple que \[[J_y, J_z] = i\hbar J_x \qquad [J_z, J_x] = i\hbar J_y\] ¿Os suena de algo? Los operadores de momento angular, en unidades de \(\hbar\), son los generadores infinitesimales de las rotaciones de SU(2), \(J_i = \frac{\hbar}{2} \sigma^{(d)}_i\) para una repr \(\mathbf{d}\). Al igual que ocurría en ese caso, también elegiremos \(J_z\) diagonal y definiremos los operadores escalera \(J_\pm = J_x \pm i J_y\) para pasar de unos autoestados a otros. También tenemos el operador de Casimir \(J^2 = {J_x}^2 + {J_y}^2 + {J_z}^2\), que conmuta con las tres componentes del momento angular. Por último, también conocíamos los autoestados del momento angular, que identificábamos mediante dos números, \(d\) que era la dimensión de la representación, y \(m\) que era el autovalor de \(\sigma_z\). En esta ocasión, por conveniencia, vamos a cambiar de notación y en vez de \(d\) vamos a usar \(j = \frac{1}{2}(d-1)\). De este modo \[J_z|j m\rangle = \hbar m |j m\rangle \qquad J^2|j m\rangle = \hbar^2 j(j+1) |j m\] Con nuestro conocimiento de SU(2), sabemos que \(m\) puede tomar \(d=2j+1\) valores distintos, comprendidos entre \(-j\) y \(j\). Además, para asegurarnos de estar en dimensión impar, \(j\) tiene que ser un número entero (y positivo, claro). Diremos que \(j\) y \(m\) son números cuánticos: \(j\) el número cuántico azimutal o de momento angular, y \(m\) el número cuántico magnético o tercera componente del momento angular. Así que automáticamente hemos visto que el momento angular está cuantizado en unidades de \(\hbar\) (como ya había obtenido heurísticamente Bohr para construir su modelo atómico), y que es el momento angular de la partícula el que determina la representación que hay que usar para las rotaciones.
La ecuación de autovalores la hemos planteado y resuelto en términos algebraicos, y con la ayuda de la teoría de grupos nos hemos defendido razonablemente. Pero, puesto que conocemos la expresión de los operadores de momento angular podríamos haber encontrado la función de onda correspondiente analíticamente, resolviendo ecuaciones diferenciales. Como el problema en cuestión tiene simetría rotacional, es conveniente utilizar unas coordenadas que reflejen esa simetría: las cartesianas no lo hacen, pero sí las esféricas, en las que cada punto está referido por una distancia al centro \(r\) y dos ángulos \(\theta\) y \(\varphi\) -piensa en latitud y longitud-. En este sistema, las autofunciones que se encuentran son los armónicos esféricos \[J_z Y_{jm}(\theta, \varphi) = \hbar m Y_{jm}(\theta, \varphi)\qquad J^2 Y_{jm}(\theta, \varphi) = \hbar^2 j(j+1) Y_{jm}(\theta, \varphi)\]
Los armónicos esféricos tienen un bonito aspecto
pero una no tan bonita expresión analítica en términos de los polinomios de Legendre:\[Y_{jm}( \theta , \varphi ) = (-1)^m \sqrt{{(2j+1)\over 4\pi}{(j-m)!\over (j+m)!}} \, P_j^m ( \cos{\theta} ) \, e^{i m \varphi } \]No os amedrentéis por esta fórmula, puesto que las propiedades importantes que se derivan de ella ya las hemos obtenido de un modo más sencillo algebraicamente.
Ahora vamos a plantear un problema que posea simetría bajo rotaciones. Para ello tendremos que resolver la ecuación de Schrödinger con un potencial que no dependa de la orientación \(V(\vec{r}) = V(r)\) (la aplicación más frecuente, aunque ni mucho menos la única, es el átomo de hidrógeno). Para resolverlo vamos a usar el mismo truco que cuando obtuvimos la ecuación de Schrödinger independiente del tiempo: dividiremos la función de ondas en dos partes, una que solo dependa del radio y otra que solo dependa de los ángulos \(\psi(r, \theta, \varphi) = u(r)v(\theta, \varphi)\):
\[\left(-\frac{\hbar^2}{2m}\nabla^2 + V(r)\right) u(r)v(\theta, \varphi) = E u(r)v(\theta, \varphi)\]
Tras unas simples manipulaciones algebraicas, se obtienen las siguientes ecuaciones:\[J^2 v(\theta, \varphi) = j(j+1) v(\theta, \varphi)\]\[\left(-\frac{\hbar^2}{2m}\frac{d^2}{dr^2} + V(r) -\frac{\hbar^2 j(j+1)}{2mr^2}\right)r u(r) = E r u(r)\]
Obviamente, la primera de las ecuaciones nos está indicando que la parte angular es un autoestado del momento, \(v(\theta, \varphi) = Y_{jm}(\theta, \varphi)\), y que por tanto los valores de \(j\) y \(m\) se conservan a lo largo del tiempo: la simetría bajo rotaciones implica la conservación del momento angular.
Esta es la expresión de la que partíamos, así que hemos hecho un giro de \(2\pi\) (muy oportuno para esta entrada). En el camino, hemos visto los generadores del grupo, y la expresión de la rotación como una exponencial. Con esta expresión hay que tener cuidado, ya que las exponenciales de matrices pueden ser traicioneras\[\exp(i \theta \hat{n}\cdot\vec{L}) = \exp[i\theta(n_xL_x + n_yL_y + n_z Lz)]\neq \exp(i\theta n_xL_x)\exp(i\theta n_y L_y)\exp(i\theta n_z L_z)\]
La exponencial de una suma de matrices está dada por la fórmula de Zassenhaus \(\exp(A+B) = \exp A \exp B \exp(-[A, B]/2) \cdots\) (a continuación vienen más conmutadores anidados). Lo que me recuerda que aún no hemos calculado el álgebra de Lie correspondiente al grupo:
\[[L_x, L_y] = i L_z \qquad [L_y, L_z]=iL_x \qquad [L_z, L_x]=iL_y\]
¿Os suena de algo? Es igual que el álgebra de Lie de SU(2), con las matrices \(\frac{1}{2}\vec{\sigma}\) -¡dichoso \(\frac{1}{2}\)-. Y allí dijimos que el álgebra de Lie determina por completo el grupo. Lo que ocurre es que determina su comportamiento para parámetros pequeños, pero no para cualquier valor: ¿Qué ocurre al hacer una "rotación" de \(2\pi\), \(\exp(i2\pi\hat{n}\cdot\frac{1}{2}\vec{\sigma})\) usando una matriz de SU(2)? Pues depende de la representación en la que nos encontremos: si es de dimensión impar \[\exp i2\pi \frac{1}{2}\sigma_z^{(3)} = \exp \begin{pmatrix} i2\pi & 0 & 0\\ 0 & 0 & 0 \\ 0 & 0 & -i2\pi\end{pmatrix} = \begin{pmatrix} e^{i2\pi} & 0 & 0\\ 0 & e^0 & 0 \\ 0 & 0 & e^{-i2\pi}\end{pmatrix} = I \]De momento, todo bien. Pero, al hacer lo mismo con las representaciones de dimensión par...\[\exp i2\pi \frac{1}{2}\sigma_z = \exp\begin{pmatrix}i\pi & 0\\ 0 & -i\pi\end{pmatrix} = \begin{pmatrix}e^{i\pi} & 0 \\ 0 & e^{-i\pi}\end{pmatrix} = -I\] Así que, para conseguir volver a la posición inicial, haría falta un giro de ¡\(4\pi\)! [Técnicamente, SU(2) es el recubrimiento doble de SO(3)]
En consecuencia, si queremos hacer la representación de una rotación en un espacio vectorial complejo, deberemos tomar una dimensión impar. Y las representaciones de dimensión par las vamos a dejar en el banquillo (de momento ;))
¡Un momento! [angular]
Llegados a este punto, quedan por resolver muchas preguntas, como por ejemplo, ¿qué cantidad conservada se asocia a la simetría bajo rotación?¿Qué representación debemos utilizar?¿Qué hago yo leyendo este artículo?Vamos a intentar dar respuesta a las dos primeras cuestiones (la tercera la tendrás que descubrir tú). Y como lo cuántico siempre es mejor -ahora que lo pienso, ese hubiera sido un buen lema para el blog - vamos a rotar las funciones de onda. Como estamos en un espacio complejo, es obvio que necesitaremos las representaciones -de dimensión impar- del buen SU(2).
Pero antes, a la cantidad conservada. Unos conocimientos a nivel usuario de la mecánica clásica son suficientes para haberse topado con el momento angular \[\vec{J} = \vec{r}\times\vec{p} = (yp_z - zp_y, zp_x - x p_z, x p_y - y p_x)\]
Para obtener su versión cuántica, no hay más que sustituir las posiciones y momentos por sus respectivos operadores \(\vec{J} = \vec{R}\times\vec{P}\). Vamos a ver qué ocurre con los conmutadores de las diferentes componentes del momento angular:
\[[J_x, J_y] = [Y P_z - Z P_y, Z P_x - X P_z] =\]\[ [Y P_z, Z P_x]+ [Y P_z, -X P_z]+ [-Z P_y, Z P_x] + [-Z P_y, -X P_z]=\]\[= YZ[P_z, P_x] + Y[P_z, Z]P_x+Z[Y, P_x]P_z+ [Y, Z]P_x P_z-\]\[ - XY[P_z, P_z] - Y[P_z, X]P_z - X[Y, P_z]P_z - [Y,X]P_zP_z\]\[-ZZ[P_y, P_x] - Z[P_y, Z]P_x - Z[Z, P_x]-[Z,Z]P_yP_x+\]\[+XZ[P_y, Pz]+Z[P_y, X]P_z + X[Z, P_z]P_y + [Z, X]P_yP_z=\]\[= Y[P_z, Z]P_x + X[Z, P_z]P_y = i\hbar(X P_y - Y P_x) = i\hbar J_z\]
Del mismo modo también se cumple que \[[J_y, J_z] = i\hbar J_x \qquad [J_z, J_x] = i\hbar J_y\] ¿Os suena de algo? Los operadores de momento angular, en unidades de \(\hbar\), son los generadores infinitesimales de las rotaciones de SU(2), \(J_i = \frac{\hbar}{2} \sigma^{(d)}_i\) para una repr \(\mathbf{d}\). Al igual que ocurría en ese caso, también elegiremos \(J_z\) diagonal y definiremos los operadores escalera \(J_\pm = J_x \pm i J_y\) para pasar de unos autoestados a otros. También tenemos el operador de Casimir \(J^2 = {J_x}^2 + {J_y}^2 + {J_z}^2\), que conmuta con las tres componentes del momento angular. Por último, también conocíamos los autoestados del momento angular, que identificábamos mediante dos números, \(d\) que era la dimensión de la representación, y \(m\) que era el autovalor de \(\sigma_z\). En esta ocasión, por conveniencia, vamos a cambiar de notación y en vez de \(d\) vamos a usar \(j = \frac{1}{2}(d-1)\). De este modo \[J_z|j m\rangle = \hbar m |j m\rangle \qquad J^2|j m\rangle = \hbar^2 j(j+1) |j m\] Con nuestro conocimiento de SU(2), sabemos que \(m\) puede tomar \(d=2j+1\) valores distintos, comprendidos entre \(-j\) y \(j\). Además, para asegurarnos de estar en dimensión impar, \(j\) tiene que ser un número entero (y positivo, claro). Diremos que \(j\) y \(m\) son números cuánticos: \(j\) el número cuántico azimutal o de momento angular, y \(m\) el número cuántico magnético o tercera componente del momento angular. Así que automáticamente hemos visto que el momento angular está cuantizado en unidades de \(\hbar\) (como ya había obtenido heurísticamente Bohr para construir su modelo atómico), y que es el momento angular de la partícula el que determina la representación que hay que usar para las rotaciones.
La ecuación de autovalores la hemos planteado y resuelto en términos algebraicos, y con la ayuda de la teoría de grupos nos hemos defendido razonablemente. Pero, puesto que conocemos la expresión de los operadores de momento angular podríamos haber encontrado la función de onda correspondiente analíticamente, resolviendo ecuaciones diferenciales. Como el problema en cuestión tiene simetría rotacional, es conveniente utilizar unas coordenadas que reflejen esa simetría: las cartesianas no lo hacen, pero sí las esféricas, en las que cada punto está referido por una distancia al centro \(r\) y dos ángulos \(\theta\) y \(\varphi\) -piensa en latitud y longitud-. En este sistema, las autofunciones que se encuentran son los armónicos esféricos \[J_z Y_{jm}(\theta, \varphi) = \hbar m Y_{jm}(\theta, \varphi)\qquad J^2 Y_{jm}(\theta, \varphi) = \hbar^2 j(j+1) Y_{jm}(\theta, \varphi)\]
Los armónicos esféricos tienen un bonito aspecto
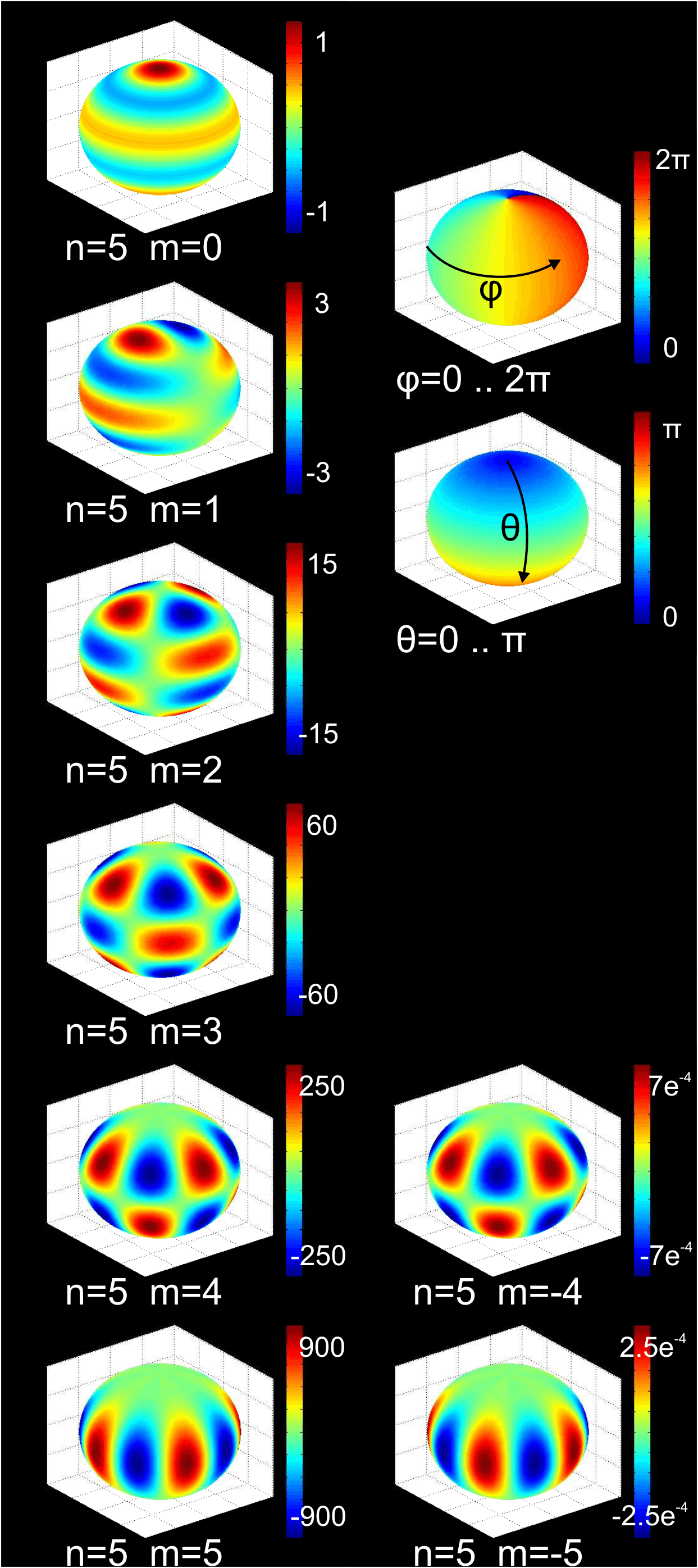 |
| Armónicos esféricos para \(j=5\) |
Ahora vamos a plantear un problema que posea simetría bajo rotaciones. Para ello tendremos que resolver la ecuación de Schrödinger con un potencial que no dependa de la orientación \(V(\vec{r}) = V(r)\) (la aplicación más frecuente, aunque ni mucho menos la única, es el átomo de hidrógeno). Para resolverlo vamos a usar el mismo truco que cuando obtuvimos la ecuación de Schrödinger independiente del tiempo: dividiremos la función de ondas en dos partes, una que solo dependa del radio y otra que solo dependa de los ángulos \(\psi(r, \theta, \varphi) = u(r)v(\theta, \varphi)\):
\[\left(-\frac{\hbar^2}{2m}\nabla^2 + V(r)\right) u(r)v(\theta, \varphi) = E u(r)v(\theta, \varphi)\]
Tras unas simples manipulaciones algebraicas, se obtienen las siguientes ecuaciones:\[J^2 v(\theta, \varphi) = j(j+1) v(\theta, \varphi)\]\[\left(-\frac{\hbar^2}{2m}\frac{d^2}{dr^2} + V(r) -\frac{\hbar^2 j(j+1)}{2mr^2}\right)r u(r) = E r u(r)\]
Obviamente, la primera de las ecuaciones nos está indicando que la parte angular es un autoestado del momento, \(v(\theta, \varphi) = Y_{jm}(\theta, \varphi)\), y que por tanto los valores de \(j\) y \(m\) se conservan a lo largo del tiempo: la simetría bajo rotaciones implica la conservación del momento angular.

No hay comentarios:
Publicar un comentario