Hoy la dirección general de tráfico ha dado a conocer datos sobre la ubicación y funcionamiento de los temidos radares móviles. Uno de ellos ha sido la publicación de los márgenes de tolerancia de los radares. Basándose en este hecho, en algunos medios de comunicación (por ejemplo, lo he visto en el programa "Más vale tarde" de la Sexta) se han preguntado si el conocimiento de estos márgenes supondrá que los conductores se dedicarán a ir al límite superior permitido por la tolerancia.
Para contestar a esta pregunta, hay que tener claro cuál es el significado de la tolerancia. Cuando un aparato realiza una medida, esta nunca puede tener una fiabilidad absoluta. Hay diversas causas que contribuyen: gran parte se debe al ruido, tanto al que afecta al objeto que se está midiendo como a los circuitos electrónicos del aparato de medida. Además, hoy en día todas las medidas se realizan mediante la conversión de señales analógicas en señales digitales: cadenas de ceros y unos de una longitud fija (bits). Si este número tiene \(n\) bits, nuestro aparato no podrá medir más que \(2^n\) valores diferentes: si está diseñado para medir en un rango de valores \(R\), no será capaz de distinguir dos medidas que difieran en \(R/2^n\).
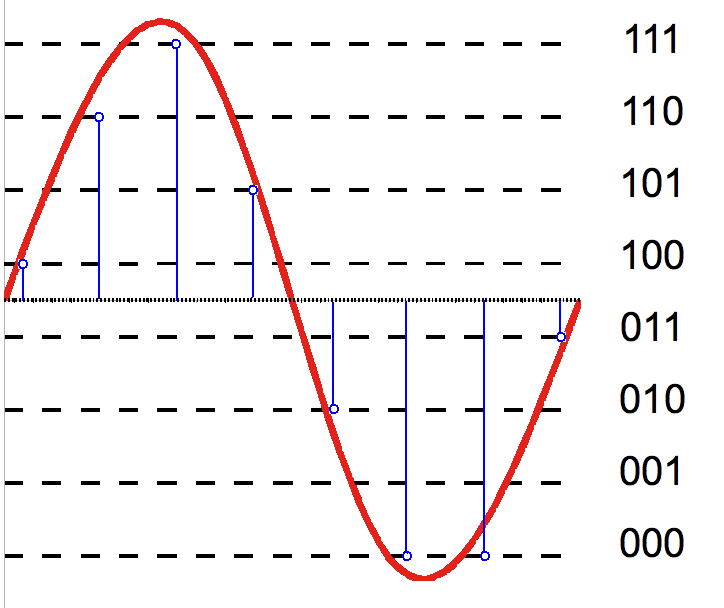 |
| Señal analógica (rojo) y digitalizada (azul) con 3 bits |
Esto significa que, cuando el aparato nos da una medida, no podemos estar seguros de que el valor que obtenemos se corresponda con el valor real del objeto que estamos midiendo. Por eso, los valores experimentales siempre se expresan con un margen de error: es el intervalo de valores reales que pueden dar lugar a la medida obtenida (o al menos, aquellos que lo hacen con mayor probabilidad).
Los radares móviles, según la DGT, en las autovías tienen un margen de error del 7%, aunque viendo los datos publicados, se corresponden al 9% (me parecen unos márgenes de error demasiado elevados para un dispositivo cuya misión sea "mejorar la seguridad", aunque como desconozco por completo los detalles de su funcionamiento, no me atrevo a opinar al respecto).
Imagínate que es un conductor circulando a 115 km/h en un tramo donde la velocidad máxima permitida es 120 km/h. Dado el margen de error del radar, eso significa que puede medir su velocidad con cualquier valor entre 107 km/h y 123 km/h. Como ves, es posible que el radar diga que has rebasado el límite de velocidad, aunque no sea cierto. Para evitar multas en estas circunstancias, el radar no "salta" a no ser que se supere el límite superior del margen de error, en este caso 131 km/h. Así que, si eres un conductor cumplidor, no tienes nada que temer de los posibles errores del radar.
Ahora vamos a responder a las dudas de los medios de comunicación: imagínate que eres un conductor "listillo" y que quieres pisarle un poco más al acelerador sin que te multen, por lo que decides ir a 128 km/h. Como vas a menos de 131 km/h no te puede pasar nada, ¿no? Error: al ir a esa velocidad, el radar puede obtener cualquier resultado entre 119 km/h y 137 km/h. Buena parte de ese rango es sancionable. Así que puede que no te multen, pero puede que sí. Solo el azar sabe cuál será el destino de tu bolsillo. (Por cierto, si quieres asegurarte de recibir en una multa, en un tramo de 120 km/h debes superar los 141 km/h).
El valor que mida el radar será uno de los del margen de error (muy probablemente). Pero eso no significa que todos los valores tengan la misma probabilidad de ser la medida del aparato: siguen una distribución de probabilidad. Los detalles de esta distribución son difíciles de conocer, ya que deberíamos tener en cuenta todas las posibles fuentes de error, lo cual es imposible (más aún sin acceso a las especificaciones del radar). Sin embargo, los matemáticos nos echan una mano con el teorema del límite central, que dice que la suma de un gran número de variables aleatorias (en este caso, todas las fuentes de error en la medida), el resultado se aproxima auna distribución normal (también conocida como gaussiana). Esto explica el hecho de que muchas de las distribuciones que se encuentren en a vida real tengan la característica forma de campana. La distribución normal es: \[P(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma ^2}}\]En esta expresión, \(P(x)dx\) es la probabilidad de obtener el valor medido entre \(x\) y \(x+dx\), \(\mu\) es el valor medio y \(\sigma\) la desviación estadística (simplemente "sigma" para los amigos), que mide la anchura de la curva.
En nuestro caso, la media es la velocidad real que llevaba el coche. La desviación estadística estará relacionada con la tolerancia. A falta de más detalles, resulta razonable asumir que la tolerancia es \(2\sigma\), con lo que el 95% de los resultados entrarían en el margen de error.\[\mu = v \qquad 2\sigma = 0.07 v\]\[P(x) = \frac{1}{0.035 v \sqrt{2\pi}}e^{-\frac{(x-v)^2}{2(0.035v)^2}}\]
La probabilidad de que el valor medido sea mayor que \(v_m\) está dada por
\[P(x > v_m) = 1 - \int_{-\infty}^{v_m} \frac{1}{0.035 v \sqrt{2\pi}}e^{-\frac{(x-v)^2}{2(0.035v)^2}} dx \]Desafortunadamente, esta integral no se puede expresar en términos de las funciones habituales. Para ello se creó la función error, definida por \[\textrm{erf}(x) = \frac{1}{\sqrt{\pi}}\int_{-x}^x e^{-t^2} d t\] Con lo cual, la probabilidad de llevarse la multa será \[P_{multa}(v) = \frac{1}{2} \left[1 - \textrm{erf} \left(\frac{v_m - v}{0.035 v \sqrt{2}}\right)\right]\]
Empleando como límite para que salte el radar \(v_m\) = 131 km/h, la probabilidad de que te cacen al ir con una velocidad \(v\) es la siguiente:
Recogemos algunos valores:
Nota: Desde este blog no pretendemos incitar a los lectores a incumplir las leyes de circulación. Recordamos que su cumplimiento es obligatorio.
Nota 2: Los valores ofrecidos aquí son meramente orientativos, y en parte son especulativos. En ningún caso nos responsabilizamos de las multas que puedan recibir los lectores.
Nota 3: Me gustaría dar las gracias a +Pedro J. Hdez por sugerir la idea que ha dado lugar a la ampliación de la entrada.
Multita o bronquita
Como sé que, pese a mis advertencias, te encomendarás a la diosa Fortuna antes que a las directrices de la DGT, voy a calcular (estimar, mejor dicho) las probabilidades de que te pille el radar.El valor que mida el radar será uno de los del margen de error (muy probablemente). Pero eso no significa que todos los valores tengan la misma probabilidad de ser la medida del aparato: siguen una distribución de probabilidad. Los detalles de esta distribución son difíciles de conocer, ya que deberíamos tener en cuenta todas las posibles fuentes de error, lo cual es imposible (más aún sin acceso a las especificaciones del radar). Sin embargo, los matemáticos nos echan una mano con el teorema del límite central, que dice que la suma de un gran número de variables aleatorias (en este caso, todas las fuentes de error en la medida), el resultado se aproxima auna distribución normal (también conocida como gaussiana). Esto explica el hecho de que muchas de las distribuciones que se encuentren en a vida real tengan la característica forma de campana. La distribución normal es: \[P(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma ^2}}\]En esta expresión, \(P(x)dx\) es la probabilidad de obtener el valor medido entre \(x\) y \(x+dx\), \(\mu\) es el valor medio y \(\sigma\) la desviación estadística (simplemente "sigma" para los amigos), que mide la anchura de la curva.
En nuestro caso, la media es la velocidad real que llevaba el coche. La desviación estadística estará relacionada con la tolerancia. A falta de más detalles, resulta razonable asumir que la tolerancia es \(2\sigma\), con lo que el 95% de los resultados entrarían en el margen de error.\[\mu = v \qquad 2\sigma = 0.07 v\]\[P(x) = \frac{1}{0.035 v \sqrt{2\pi}}e^{-\frac{(x-v)^2}{2(0.035v)^2}}\]
La probabilidad de que el valor medido sea mayor que \(v_m\) está dada por
\[P(x > v_m) = 1 - \int_{-\infty}^{v_m} \frac{1}{0.035 v \sqrt{2\pi}}e^{-\frac{(x-v)^2}{2(0.035v)^2}} dx \]Desafortunadamente, esta integral no se puede expresar en términos de las funciones habituales. Para ello se creó la función error, definida por \[\textrm{erf}(x) = \frac{1}{\sqrt{\pi}}\int_{-x}^x e^{-t^2} d t\] Con lo cual, la probabilidad de llevarse la multa será \[P_{multa}(v) = \frac{1}{2} \left[1 - \textrm{erf} \left(\frac{v_m - v}{0.035 v \sqrt{2}}\right)\right]\]
Empleando como límite para que salte el radar \(v_m\) = 131 km/h, la probabilidad de que te cacen al ir con una velocidad \(v\) es la siguiente:
Recogemos algunos valores:
- A 120 km/h, probabilidad del 0.44%
- A 125 km/h, probabilidad del 8.5%
- A 130 km/h, probabilidad del 41.3%
- A 135 km/h, probabilidad del 80.1%
- A 140 km/h, probabilidad del 96.7%
- A 145 km/h, probabilidad del 99.7%
Nota: Desde este blog no pretendemos incitar a los lectores a incumplir las leyes de circulación. Recordamos que su cumplimiento es obligatorio.
Nota 2: Los valores ofrecidos aquí son meramente orientativos, y en parte son especulativos. En ningún caso nos responsabilizamos de las multas que puedan recibir los lectores.
Nota 3: Me gustaría dar las gracias a +Pedro J. Hdez por sugerir la idea que ha dado lugar a la ampliación de la entrada.



No hay comentarios:
Publicar un comentario