Para la entrada de hoy vamos a viajar un poco hacia atrás en el tiempo. Algo más de trecemil millones de años, concretamente. Eran tiempos interesantes, y aunque no los pudimos ver de primera mano, tenemos fuertes indicios de lo que "se cocía". Uno de ellos es la Nucleosíntesis del Big Bang (BBN). La formulación teórica se encuentra en el artículo "\(\alpha\beta \gamma \)" (Alpher-Bethe-Gamow). Antes de entrar en materia, la anécdota detrás de este artículo: la investigación la realizó el conocido físico ruso-americano George Gamow junto a su estudiante de doctorado Ralph Alpher. Pero Gamow era un graciosillo, y consideró que la lista de autores quedaría más redonda si completara el alfabeto griego invitando a Hans Bethe, físico nuclear y amigo personal de Gamow. Bethe no intervino en el articulo, pero curiosamente le tocó revisarlo para su publicación en Physical Review. A Alpher no le hizo ninguna gracia, porque pensaba que al compartir autoría con no uno sino dos de los mejores físicos del momento, se minusvaloraría su aportación. Posteriormente Bethe se interesaría por la nucleosíntesis, no la del Big Bang, sino la estelar, lo que le valdría el premio Nobel.
El universo se está expandiendo, lo que aplicando termodinámica básica significa que se está enfriando. En los primeros instantes, la temperatura era tan elevada que los gluones no estaban confinados por la QCD, y constituían un plasma de quarks y gluones. Las partículas tenían tanta energía que en las colisiones se creaban y destruían materia y antimateria en equilibrio.
Cuando la energía térmica (\( k_B T\)) cayó por debajo de la masa de las partículas (\( m c^2\)), el equilibrio se rompió y solo fueron posibles las reacciones de aniquilación de materia y antimateria. En este punto no tenemos muy claro por qué la materia "ganó" a la antimateria (bariogénesis).
Sólo han transcurrido unos milisegundos desde el Big Bang, y ya solo tenemos quarks y electrones, y además los quarks ya pueden formar hadrones. Inicialmente había tantos protones como neutrones. Protones y neutrones estaban en equilibrio debido a la reacción débil \( p + e^- \leftrightarrow n + \bar{\nu}_e\). Una vez más el equilibrio se rompió, decantándose por la creación de protones. Teniendo en cuenta además que los neutrones libres son inestables, con una vida media de un cuarto de hora, acabamos con un neutrón por cada siete protones.
Han pasado unos diez segundos desde el Big Bang, y la temperatura ya es suficientemente "fresquita" para permitir reacciones nucleares. ¡Empieza la nucleosíntesis! Las primeras reacciones, claro está, son de un protón con un neutrón para dar un núcleo de deuterio (\(^2H\)). El deuterio se puede combinar con un protón para formar \(^3He\) o con un neutrón para formar tritio (\(^3H\), es radiactivo). Y por supuesto dos núcleos de deuterio pueden formar nuestro protagonista, el \(^4He\). Para comprender plenamente su importancia necesitaremos la siguiente gráfica:
Sólo han transcurrido unos milisegundos desde el Big Bang, y ya solo tenemos quarks y electrones, y además los quarks ya pueden formar hadrones. Inicialmente había tantos protones como neutrones. Protones y neutrones estaban en equilibrio debido a la reacción débil \( p + e^- \leftrightarrow n + \bar{\nu}_e\). Una vez más el equilibrio se rompió, decantándose por la creación de protones. Teniendo en cuenta además que los neutrones libres son inestables, con una vida media de un cuarto de hora, acabamos con un neutrón por cada siete protones.
Han pasado unos diez segundos desde el Big Bang, y la temperatura ya es suficientemente "fresquita" para permitir reacciones nucleares. ¡Empieza la nucleosíntesis! Las primeras reacciones, claro está, son de un protón con un neutrón para dar un núcleo de deuterio (\(^2H\)). El deuterio se puede combinar con un protón para formar \(^3He\) o con un neutrón para formar tritio (\(^3H\), es radiactivo). Y por supuesto dos núcleos de deuterio pueden formar nuestro protagonista, el \(^4He\). Para comprender plenamente su importancia necesitaremos la siguiente gráfica:
¿Cómo afecta esto a nuestro Universo en pañales? Podemos suponer que, en primera aproximación, la nucleosíntesis es únicamente la creación de \(^4He\) partiendo de protones y neutrones. En este caso el factor limitante es la cantidad de neutrones: Ya hemos dicho que, de cada 8 nucleones, 7 son protones y el otro un neutrón. Por cada neutrón necesitamos un protón ligado en el núcleo de helio. Los otros 6 protones quedan libres. Es decir, que una cuarta parte de los nucleones tras la nucleosíntesis forman helio-4 y el resto hidrógeno.
Unos cálculos más detallados tienen en cuenta la producción de otros isótopos, principalmente deuterio, helio-3 y litio-7, además de los radiactivos tritio y berilio-7. Los valores de las abundancias de estos elementos dependen únicamente de la proporción bariones/fotones, \(\eta\). Este parámetro es muy importante en cosmología, ya que nos permite adentrarnos en los primeros instantes del Universo y conocer qué proporción de la materia es baríónica (es decir, no oscura). El hecho de que el valor de \(\eta\) calculado para cada uno de estos elementos coincida, y también con el valor obtenido de forma independiente por los satélites WMAP y Planck, es la principal - de las muchas- evidencias en favor del modelo del Big Bang.
¿Y qué hay del resto de elementos más pesados? Teniendo en cuenta que casi todo el Universo era hidrógeno y helio-4, cabría esperar colisiones \(^1 H+{}^4He\) y \(^4He+{}^4He\). Pero si vuelves a la gráfica de energía de enlace por nuclear, no verás ningún isótopo con 5 o con 8 nucleones. Y es que estos isótopos no son estables (les sale más rentable desintegrarse a helio-4 que tener que aguantarse). Así que para hacer elementos más pesados habrá que partir del litio-7, usando \(^7Li +{}^2H\to {}^9Be\) y \(^7Li + {}^4He\to{}^{11}B\). El problema es que el litio es muy escaso, representando una parte en \(10^9\) de la masa del Universo. El tiempo tampoco estaba de nuestra parte, ya que a los 20 minutos del Big Bang la temperatura era demasiado baja para permitir reacciones nucleares, y la nucleosíntesis terminó. Al final sólo se había producido una parte en \(10^{16}\) de berilio y boro, y de elementos más pesados nada de nada.
Para ello tendremos que esperar unos millones de años a las primeras estrellas. Las extremas condiciones de su interior permiten crear carbono a partir de tres helios-4, y reacciones de fusión nuclear hasta llegar al hierro y níquel. Los elementos más pesados se originan en las explosiones de supernova. Pero eso es otra historia, y debe ser contada en otra ocasión.
 |
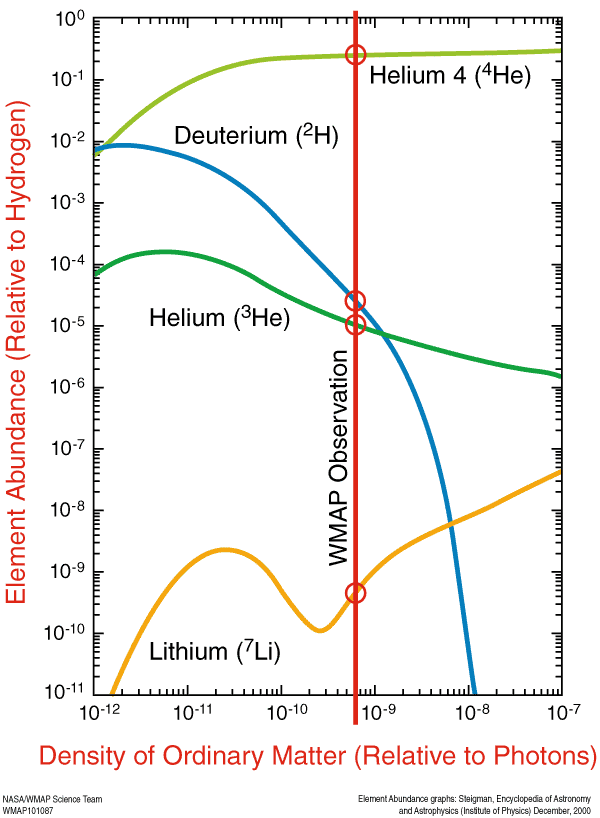| Abundancia de los elementos en función de \(\eta\) (WMAP / NASA) |
Unos cálculos más detallados tienen en cuenta la producción de otros isótopos, principalmente deuterio, helio-3 y litio-7, además de los radiactivos tritio y berilio-7. Los valores de las abundancias de estos elementos dependen únicamente de la proporción bariones/fotones, \(\eta\). Este parámetro es muy importante en cosmología, ya que nos permite adentrarnos en los primeros instantes del Universo y conocer qué proporción de la materia es baríónica (es decir, no oscura). El hecho de que el valor de \(\eta\) calculado para cada uno de estos elementos coincida, y también con el valor obtenido de forma independiente por los satélites WMAP y Planck, es la principal - de las muchas- evidencias en favor del modelo del Big Bang.
¿Y qué hay del resto de elementos más pesados? Teniendo en cuenta que casi todo el Universo era hidrógeno y helio-4, cabría esperar colisiones \(^1 H+{}^4He\) y \(^4He+{}^4He\). Pero si vuelves a la gráfica de energía de enlace por nuclear, no verás ningún isótopo con 5 o con 8 nucleones. Y es que estos isótopos no son estables (les sale más rentable desintegrarse a helio-4 que tener que aguantarse). Así que para hacer elementos más pesados habrá que partir del litio-7, usando \(^7Li +{}^2H\to {}^9Be\) y \(^7Li + {}^4He\to{}^{11}B\). El problema es que el litio es muy escaso, representando una parte en \(10^9\) de la masa del Universo. El tiempo tampoco estaba de nuestra parte, ya que a los 20 minutos del Big Bang la temperatura era demasiado baja para permitir reacciones nucleares, y la nucleosíntesis terminó. Al final sólo se había producido una parte en \(10^{16}\) de berilio y boro, y de elementos más pesados nada de nada.
Para ello tendremos que esperar unos millones de años a las primeras estrellas. Las extremas condiciones de su interior permiten crear carbono a partir de tres helios-4, y reacciones de fusión nuclear hasta llegar al hierro y níquel. Los elementos más pesados se originan en las explosiones de supernova. Pero eso es otra historia, y debe ser contada en otra ocasión.
No hay comentarios:
Publicar un comentario