La Qubit_era

Hoy en dia, hay problemas matemáticos que no son resolubles en los ordenadores "tradicionales". Hasta tal punto que la seguridad de nuestras comunicaciones por internet (incluyendo todas las transacciones bancarias) depende de esta incapacidad. El problema no está en que hagan falta procesadores más potentes. Son limitaciones de la arquitectura de un ordenador clásico. Para superarlas, necesitamos un nuevo tipo de ordenadores: los ordenadores cuánticos.

En primer lugar debemos tener bien claro qué es un ordenador cuántico. No es suficiente con que algunos de sus componentes sean cuánticos. Al fin y al cabo, los transistores y diodos que componen un ordenador electrónico deben su funcionalidad a la mecánica cuántica. La diferencia esencial se encuentra en el modo de representar y operar con la información.

En un ordenador usual, la unidad básica de información es el bit. Un bit puede tomar los valores 0 o 1: sí o no, blanco o negro, cara o cruz. Físicamente un bit se puede implementar como el modo de un transistor, la dirección de la imanación en un disco duro o la profundidad de un surco en un DVD, por ejemplo.

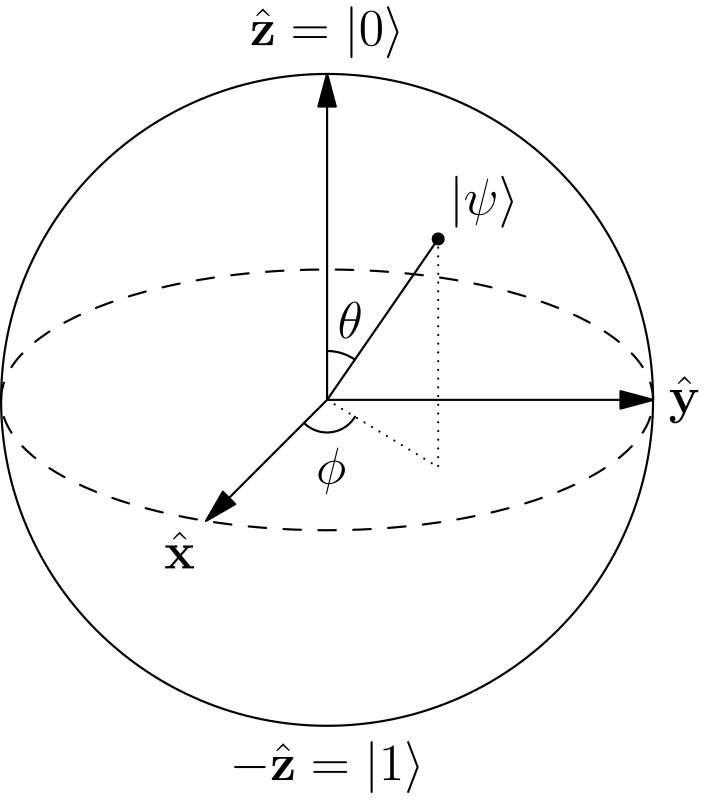
Un ordenador cuántico, por contra, emplea qubits. Un qubit es el estado cuántico de un sistema de dos niveles, a los que denominaremos \(|0\rangle\) y \(|1\rangle\). Un aspecto clave de la mecánica cuántica es que las superposiciones (combinaciones lineales) de estados están permitidas. Así pues, un qubit puede estar en cualquier superposición \[ |\psi\rangle = \alpha |0\rangle + \beta |1\rangle \]Esto significa que un qubit puede tener muchos estados. Usualmente estos se representan mediante la esfera de Bloch: los polos son los estados de la base, y la superficie esférica sus superposiciones.

El gran poder de la computación cuántica radica precisamente en la superposición: si realizamos una operación sobre un qubit \(|\psi\rangle\), la estamos realizando simultáneamente sobre los dos estados \(|0\rangle\) y \(|1\rangle\). Si quisiéramos hacer lo mismo con un bit, computar los resultados de una operación sobre los estados 0 y 1, deberíamos ejecutar la operación dos veces. La cosa se pone interesante si añadimos más qubits entrelazados: con \(N\) de ellos podemos realizar simultáneamente el equivalente a \(2^N\) operaciones clásicas. ¡Todo un chollo!

Ahora la cuestión es fabricar sistemas físicos que se comporten como qubits: algunas de las posibilidades son la polarización de un fotón, el espín de un electrón o de un núcleo, o la corriente en un superconductor. 

Las principales características que debe poseer un qubit son:

• Posibilidad de manipular el estado. Las operaciones se realizan mediante puertas lógicas cuánticas, que actúan de forma unitaria (reversible). Su implementación física depende del tipo de qubit empleado. Por ejemplo, si se usan átomos en una trampa óptica, su estado se puede modificar con láseres y vibraciones de la red atómica.
• Inmunidad frente a la decoherencia: Los qubits tienen la manía de interaccionar con el ambiente y entrelazarse con él. Como consecuencia, transcurrido un tiempo \(T_2\) (tiempo de decoherencia) el qubit pierde la superposición y se comporta como un bit clásico.

La lucha contra la de coherencia es el principal obstáculo a superar para construir un ordenador cuántico. Los tiempos de decoherencia típicos suelen ser del orden de microsegundos, aunque en ciertas condiciones se pueden conseguir incluso horas.

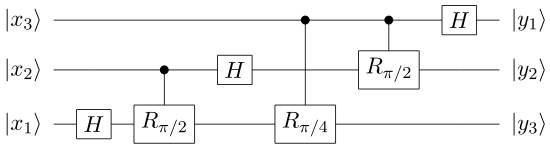
También se han desarrollado algunos algoritmos para ordenadores cuánticos, que superan a su equivalente clásico, como la transformada de Fourier. El ejemplo más importante es el algoritmo de Shor, que permite descomponer en factores primes un número de manera eficiente (y así romper el cifrado RSA).