Un Universo a mi medida

¿Por qué limitarse a estudiar los efectos gravitatorios de una estrella, como había hecho Schwarzschild? La nueva ecuación de Einstein permitía describir la forma y dinámica del Universo en su conjunto. Con la relatividad general nació la cosmología como ciencia.

Einstein y su Universo

Y el primero que se lanzó a la cosmología en 1917 fue el propio Einstein. Las características en las que basó su modelo fueron:

• Distribución homogénea e isótropa de la materia y energía, modelado como un fluido. Si bien es cierto que en la vida real la materia se agolpa en estrellas, cúmulos y galaxias, cuando se ve a escalas cósmicas estas "irregularidades" se suavizan.
• Universo con forma esférica
• Eterno, y sin ninguna evolución temporal.

Sin embargo, cuando resolvió las ecuaciones correspondientes a un fluido homogéneo e isótropo, se encontró con una desagradable sorpresa: ¡era imposible obtener un universo estático! En su lugar, se expandía o se contraía. Para remediar este problema, Einstein se vio forzado a modificar sus ecuaciones de campo, incluyendo un término conocido como constante cosmológica \(\Lambda\). Esta modificación es perfectamente compatible con los postulados de la relatividad general (de hecho, resulta que es la única modificación permisible):\[R_{\mu\nu}-\frac{1}{2}R g_{\mu\nu}+ \Lambda g_{\mu\nu} = \frac{8\pi G}{c^4}T_{\mu\nu}\]Para comprender el significado de este nuevo término, podemos pasarlo al otro lado de la igualdad e interpretarlo como una nueva contribución al tensor energía-momento: pero no es una energía asociada a la materia, sino al espaciotiempo mismo: la energía del vacío.

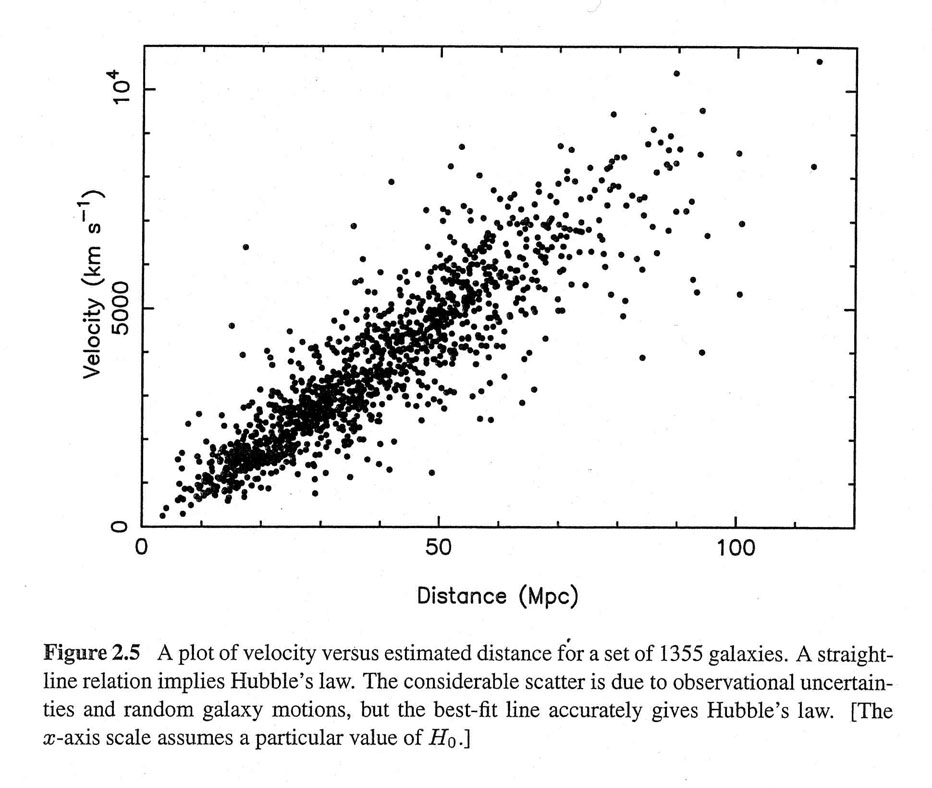
La constante cosmológica parecía solucionar los problemas de Einstein. Sin embargo, el cura belga George Lemaître mostró que el universo de Einstein era inestable. Pocos años después, Hubble descubrió que el Universo estaba compuesto por galaxias, y que estas se estaban separando: las galaxias más lejanas se separan a mayor velocidad que las cercanas \[v = H d\]

Con este nuevo descubrimiento, Einstein abandonó su universo estático y renegó de su constante cosmológica ("the biggest blunder of my life").

La expansión del Universo y el Big Bang

Incluso antes del descubrimiento de Hubble, Lemaître ya había descubierto la ley de expansión del Universo. Esta solución fue descubierta posteriormente y de manera independiente por más gente, por lo que hoy se conoce como la métrica de Friedmann-Lemaître-Robertson-Walker (o alguna otra combinación de estos nombres): \[ds^2 = g_{\mu\nu}dx^\mu dx^\nu = -c^2 dt^2 + a(t)^2\left[\frac{dr^2}{1-kr^2} + r^2 d\theta^2 + r^2\sin^2 \theta d\phi^2\right] \]

No es tan complicado como parece... El término entre corchetes es la métrica (la regla para medir ángulos y distancias) de un espacio tridimensional, fijando el tiempo. \(k\) es la curvatura espacial (que no espaciotemporal, ojo): con \(k =0\) el espacio es plano, con \(k>0\) esférico y con \(k<0\) hiperbólico. Las distancias medidas con esta métrica hay que "corregirlas" mediante el factor de escala \(a(t )\), que depende del tiempo pero no del espacio. Es decir, dados dos puntos del espacio, la distancia entre ellos cambia aunque no cambien sus coordenadas.

El factor de escala cambia con el tiempo según las ecuaciones de Friedmann, que son el resultado de aplicar la ecuación de Einstein con la métrica FLRW y un fluido de densidad \(\rho\) y presión \(p\):

\[H^2 = \left(\frac{\dot{a}}{a}\right)^2 = \frac{8 \pi G}{3}\rho - \frac{kc^2}{a^2}\\\dot{H} + H^2 = \frac{\ddot{a}}{a} = - \frac{4\pi G}{3}\left(\rho + \frac{3p}{c^2}\right)\]

El fluido cósmico lo podemos caracterizar por su ecuación de estado \(p = w \rho c^2\) (no es más que la típica ecuación de los gases perfectos):

• La radiación (fotones, neutrinos, y demás partículas con velocidades relativistas) tiene \(w=1/3\), con lo que el factor de escala aumenta según \(a(t)\sim \sqrt{t}\). Con la expansión, su densidad disminuye debido al distanciamiento de los fotones y a su corrimiento al rojo (la expansión aumenta la longitud de onda).
  
• El polvo (materia ordinaria y materia oscura, con velocidades no relativistas) tiene \(w= 0\), así que el factor de escala aumenta más rápidamente, \(a(t)\sim t^{3/2}\). Con la expansión, su densidad disminuye debido al distanciamiento de las partículas.
  
  
• A la energía del vacío le correspondería \(w=-1\), por lo que conseguimos una expansión exponencial \(a(t)\sim\exp(Ht)\). Con la expansión, su densidad se mantiene constante.
  

Si el factor de escala crece con el tiempo, rebobinando encontramos un tiempo en el que \(a= 0\): ¡no podemos medir distancias!. Lemaître descubrió esta singularidad y la bautizó como "huevo cósmico", aunque el nombre que ha pasado a la historia fue propuesto por el mayor detractor de la teoría, Fred Hoyle, para ridiculizarla: Big Bang.

El Universo tal y como lo vemos

La observación de supernovas tipo Ia reveló que la expansión del Universo no sucede tal y como dice la ley de Hubble, con un parámetro \(H\) constante, sino de forma acelerada. Esta expansión no se puede conseguir en las ecuaciones de Friedmann con radiación o polvo. Hace falta otro tipo de fluido, la energía oscura \(w<0\). Entre los candidatos a energía oscura está la resucitada constante cosmológica de Einstein y la quintaesencia.

Los resultados obtenidos por la misión Planck apuntan a un Universo plano y principalmente compuesto por energía oscura, muy probablemente en forma de constante cosmológica. La expansión acelerada es relativamente reciente, ya que antes el polvo (y mucho antes la radiación) dominaba.