Cualquier agujero negro es trinchera

La ecuación de campo de Einstein, una vez que se plantea para una geometría determinada, se convierte en un conjunto de diez ecuaciones diferenciales de segundo grado no lineales acopladas. Sí, da tanto miedo como aparenta. Tanto es así que Einstein para sus predicciones había empleado solamente una aproximación, y creía que era completamente imposible encontrar una solución exacta a su portentosa ecuación.

Sin embargo, se equivocó, y la primera solución solo tardó algo más de un mes en aparecer. La encontró Karl Schwarzschild, que había sido director del observatorio de Göttingen. Al declararse la primera Guerra Mundial, se alistó voluntariamente en el ejército alemán y llegó a ser teniente de artillería. Se encontraba en el frente ruso cuando leyó el artículo de Einstein y encontró la primera solución a su ecuación. Poco después murió debido a una enfermedad cutánea llamada pénfigo.

Schwarzschild supuso una métrica estática y con simetría esférica respecto a un punto. Empleó un universo vacío \(T_{\mu\nu} =0\). Por lo tanto, su solución describe un espaciotiempo con una masa puntual \(M\) concentrada en el centro. La métrica que obtuvo era

\[d s^2 = g_{\mu\nu}dx^\mu dx^\nu = - \left(1-\frac{2GM}{c^2 r}\right)c^2 dt^2 + \frac{1}{1-\frac{2GM}{c^2 r}}dr^2 + r^2d\theta^2 + r^2 \sin^2\theta d\phi^2 \]

En primer lugar se puede comprobar que, cuando el campo es suficientemente débil, se aproxima por el potencial gravitatorio newtoniano de una masa puntual \[\Phi \approx -\frac{1}{2}(g_{00}+c^2) = -\frac{GM}{r}\]

Más aún, cuando nos alejamos mucho del centro, vemos un espaciotiempo plano.

Si nos adentramos un poco más, vemos que empiezan a pasar cosas raras al llegar a \[r = R_S = \frac{2GM}{c^2}\] aquí la componente temporal de la métrica se anula y la espacial se hace infinita. Pero no pasa nada grave. El problema es que hemos escogido unas coordenadas poco adecuadas para describir esta zona (lo mismo que pasa en muchos mapas que fallan al representar los polos). Pero los invariantes, como la curvatura, están perfectamente definidos, y existen otras coordenadas que sí que se comportan bien (por ejemplo, las de Kruskal).

Una vez pasado el punto conflictivo \(r = R_S\) nos encontramos con un hecho sorprendente: ¡el radio y el tiempo han intercambiado sus papeles! Ahora el radio lleva el signo negativo en la métrica y el tiempo el positivo. Esto significa que, si antes era irremediable avanzar en el tiempo, ahora es irremediable acercarse más y más al centro. Ya no hay vuelta atrás. Efectivamente, hemos entrado en el agujero negro, y en \(r = R_S\) se encontraba el horizonte de sucesos, el punto de no-retorno.

Siguiendo rumbo al centro, encontramos que en \(r=0\) la métrica se hace de nuevo infinita. Pero esta vez no tenemos tanta suerte. Aquí la curvatura es infinita. Estamos en la temida singularidad. Si la Relatividad General es la teoría definitiva, significa que en este punto dejan de ser válidas por completo las leyes de la física. El fin.

Los agujeros negros de Schwarzschild son los más simples que podemos concebir, pero no los únicos. También pueden poseer momento angular y/o carga eléctrica, y la descripción más general es la métrica de Reissner-Nordström. El teorema de no-pelo prohíbe que los agujeros negros tengan cualquier otra propiedad medible desde su exterior.

En un principio se creyó que cualquier objeto responsable de un campo gravitatorio esférico tendría un radio mucho mayor que el correspondiente radio de Schwarzschild, por lo que el horizonte de sucesos y su interior serían simplemente curiosidades matemáticas. Pero Oppenheimer mostró que una estrella de neutrones con una masa superior a tres masas solares acabaría colapsando gravitatoriamente sin límite, formando un agujero negro.

Actualmente hay bastantes evidencias en favor de los agujeros negros de origen estelar, principalmente debido a la radiación emitida por los objetos al ser acretados por el agujero negro y al efecto sobre sus compañeras binarias. El ejemplo clásico es Cygnus X-1.

Emisión en rayos X del disco de acrección en torno a Cygnus X-1. Imagen: Telescopio Chandra (NASA)

También es casi segura la existencia de agujeros negros supermasivos en el centro de algunas (si no casi todas) las galaxias. En el caso de la Vía Láctea, nuestro agujero negro supermasivo es Sagittarius A*, que se hace patente por las trayectorias que describen las estrellas que pasan por el centro galáctico. Su mecanismo de formación no está muy claro.

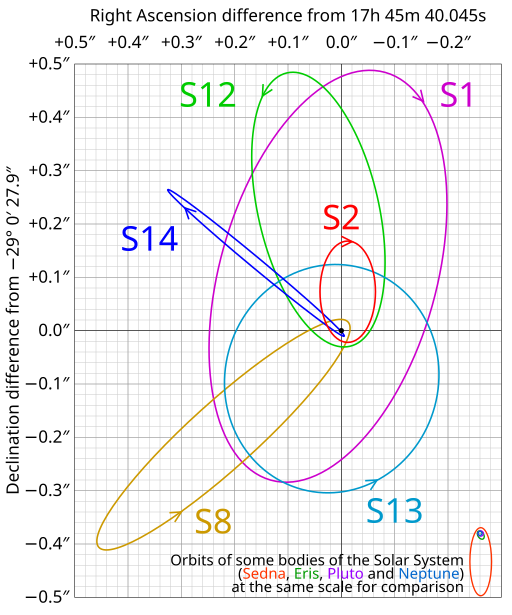Órbitas de algunas estrellas en torno a Sagittarius A*

Hay otros tipos de agujeros negros que resultan más polémicos. Tenemos los agujeros negros primordiales, que se habrían formado justo tras el Big Bang en regiones donde la densidad de materia sería ligeramente superior. Y también los microagujeros negros, formados en colisiones de partículas muy energéticas (como en el LHC o los rayos cósmicos) y que se evaporarían rápidamente en forma de radiación Hawking. En ambos casos no hay suficientes evidencias de su existencia.