"La carrera de un joven físico teórico consiste en tratar el oscilador armónico en sucesivos grados de abstracción" - Sidney Coleman
El oscilador armónico es uno de los sistemas más simples que se pueden encontrar en física. Sin embargo, es prácticamente omnipresente, desde un simple muelle hasta las más avanzadas teorías cuánticas de campos. La razón de esto es que cualquier partícula, en las proximidades de un mínimo de energía, sufre un potencial de tipo armónico:
\[V(x) \approx V(x_0) + \frac{\partial V}{\partial x}\big|_{x=x_0} + \frac{1}{2}\frac{\partial^2 V}{\partial x^2}\big|_{x=x_0} x^2 + ... \equiv \frac{1}{2} k x^2 \] (el término constante \(V(x_0)\), como ya vimos, es irrelevante, y la primera derivada se anula porque hay un mínimo en \(x=x_0\)).
El movimiento de una partícula clásica sometida a este potencial es muy sencillo. Vamos a obtenerlo usando el formalismo lagrangiano:\[L = T-V = \frac{1}{2} m \dot{x}^2 - \frac{1}{2}kx^2\]
\[\frac{\partial}{\partial t}\frac{d L}{d\dot{x}} = m \ddot{x} = \frac{d L}{d x} = -k x\]\[x(t) = A \cos \sqrt{\frac{k}{m}}t + B\sin \sqrt{\frac{k}{m}} t\]
La partícula describe un movimiento periódico de frecuencia [angular] \(\omega = \sqrt{\frac{k}{m}}\), de modo que \(x(t_0 + 2\pi/\omega) = x(t_0)\).
Pásate al lado cuántico de la fuerza
Las cosas empiezan a ponerse interesantes si cuantizamos este invento. Ya vimos cómo construir el hamiltoniano cuántico partiendo de uno clásico elsewhere. Así que la ecuación de Schrödinger (independiente del tiempo) es tan simple como:
\[H\psi = \left(\frac{1}{2m}P^2 + \frac{1}{2}kX^2\right)\psi = \left(\frac{-\hbar^2}{2m}\frac{d}{dx} + \frac{1}{2}m\omega^2 x^2\right)\psi = E \psi \]
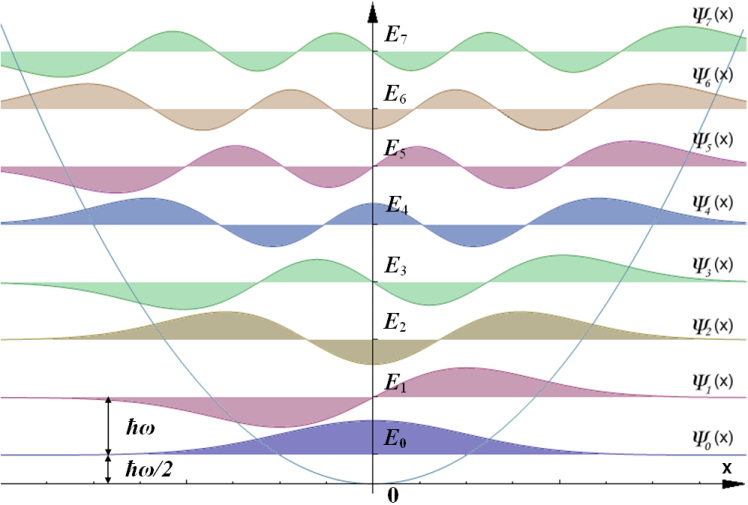
Es una bonita ecuación diferencial de segundo orden que tiene solución analítica (lo cual no suele ser muy corriente en la cuántica), como producto de un polinomio de Hermite y una función gaussiana. Naturalmente, resolverlo así es bastante tedioso. Por si tienes interés, las funciones de onda resultantes tienen el aspecto:
A crear y destruir
Vamos a solucionarlo de otro modo. Y solo vamos a utilizar el hecho de que \([X, P] = i\hbar\):
Para empezar vamos a adimensionalizar los operadores. Una ecuación expresada en términos de las escalas características del problema siempre es más elegante, y usualmente más fácil de resolver. Para el momento:
\[\frac{P_0^2}{2m} = E_0 = \hbar \omega \qquad \Longrightarrow \qquad P_0 = \sqrt{2m\hbar\omega}\]
y para la posición:
\[\frac{1}{2}m\omega^2 X_0^2 = E_0 = \hbar\omega \qquad \Longrightarrow\qquad X_0 = \sqrt{\frac{2 \hbar}{m\omega}}\]
\[K = \frac{P}{P_0} = \frac{P}{\sqrt{2m\hbar\omega}}\qquad Q = \frac{X}{X_0} = X \sqrt{\frac{m\omega}{2\hbar}}\]
Su conmutador es:
\[[Q, K] =\sqrt{\frac{m\omega}{2\hbar}}\frac{1}{\sqrt{2m\hbar\omega}}[X, P] = \frac{i}{2}\]
y podemos expresar el hamiltoniano con estos operadores:
\[H = \hbar\omega(K^2+Q^2)\]
Como \(Q\) y \(K\) tienen las mismas dimensiones (son adimensionales) podemos sumarlos sin problemas. Así que vamos a definir los siguientes operadores:\[a = Q + i K \qquad a^\dagger Q - i K \qquad Q = \frac{1}{2}(a+a^\dagger) \qquad K = \frac{1}{2i}(a-a^\dagger)\]
El conmutador de estos dos operadores es
\[[a,a^\dagger]=[Q+iK, Q-iK]= i[K,Q]-i[Q,K] =1\]
Y el hamiltoniano es
\[H = \hbar\omega(K^2+Q^2) =\frac{1}{4}\hbar\omega(-a^2+aa^\dagger +a^\dagger a - {a^\dagger}^2 + a^2+ aa^\dagger +a^\dagger a +{a^\dagger}^2) =\]\[= \hbar\omega\left(a^\dagger a +\frac{1}{2}\right)\]
\[a^\dagger a = aa^\dagger - 1 = \frac{1}{\hbar\omega}\left(H-\frac{1}{2}\right)\]
Ahora vamos a buscar a los autovectores y autovalores de la energía. Denotaremos a los autovectores con \(|v\rangle\) (ket), y a su conjugado como \(\langle v|\) (bra. El nombre se lo inventó Dirac, que era inglés, y por lo tanto supongo que conocía el significado de la palabra en su idioma). Para la integral \(\int v^\star w dx\) usaremos \(\langle v|w\rangle\) (braket).
 |
| Imagen a cargo de Tippe Top Physics (@ttphysics) |
Supongamos que conocemos uno de estos autovectores, \(|\varepsilon_0\rangle\), tal que \(H|\varepsilon_0\rangle = \varepsilon_0|\varepsilon_0\rangle\) vamos a ver qué les ocurre a los vectores \(|\varepsilon_+ \rangle = a^\dagger |\varepsilon_0\rangle\) y \(|\varepsilon_-\rangle = a|\varepsilon_0\rangle\) al aplicarles el hamiltoniano:
\[H|\varepsilon_+\rangle = \hbar\omega\left(a^\dagger a +\frac{1}{2}\right) a^\dagger |\varepsilon_0\rangle = \hbar\omega a^\dagger (a a^\dagger)|\varepsilon_0\rangle + \frac{1}{2}\hbar\omega a^\dagger |\varepsilon_0\rangle =\]\[= \hbar\omega a^\dagger (a^\dagger a +1)|\varepsilon_0\rangle + \frac{1}{2}\hbar\omega a^\dagger |\varepsilon_0\rangle = a^\dagger H |\varepsilon_0\rangle + \hbar \omega a^\dagger |\varepsilon_0\rangle =\]\[= (\varepsilon_0 + \hbar\omega) a^\dagger |\varepsilon_0\rangle = (\varepsilon_0 + \hbar\omega)|\varepsilon_+\rangle\]
\[H|\varepsilon_-\rangle = \hbar\omega\left(a^\dagger a + \frac{1}{2}\right)a|\varepsilon_0\rangle = \hbar\omega(aa^\dagger-1)|\varepsilon_0\rangle + \frac{1}{2}\hbar \omega a|\varepsilon_0\rangle = \]\[=\hbar\omega a (a^\dagger a)|\varepsilon_0\rangle - \frac{1}{2}\hbar\omega a|\varepsilon_0\rangle = a H |\varepsilon_0\rangle - \hbar\omega a|\varepsilon_0\rangle = \]\[(\varepsilon_0 - \hbar\omega)a|\varepsilon_0\rangle = (\varepsilon_0 - \hbar\omega)|\varepsilon_-\rangle\]
Así pues, \(|\varepsilon_+\rangle\) y \(|\varepsilon_-\rangle\) también son autoestados del hamiltoniano, con energías \(\varepsilon_\pm = \varepsilon_0 \pm \hbar \omega\). Haciendio actuar de nuevo los operadores \(a\) y \(a^\dagger\) se consigue un conjunto de autoestados con energías equiespaciadas en \(\hbar\omega\). Por ello, se les conoce como operadores de creación y destrucción, o escalera: crean o eliminan un cuanto de energía del oscilador.
Pero, ¿tiene algún limite la escalera de autoestados? La respuesta es que sí, tiene un límite inferior. Para comprobarlo, no hace falta más que ver lo siguiente:
\[\varepsilon_0 - \frac{1}{2}\hbar\omega = \langle \varepsilon_0|a^\dagger a|\varepsilon_0\rangle = \int \varphi^\star_0 a^\dagger a \varphi dx = \int |a\varphi_0|^2 dx \geq 0 \]
\[\varepsilon_0 \geq \frac{1}{2}\hbar\omega\]
Así que tiene que haber una energía mínima. Esta energía corresponderá a un autoestado, al que llamaremos estado fundamental o ground state, y lo denotaremos como \(|0\rangle\). Para que la escalera de energías acabe en él, tenemos que asegurarnos de que el operador de destrucción, en vez de llevarnos a otro autoestado, acabe por completo con la función de ondas:\[a|0\rangle = 0\]Con esta propiedad podemos obtener la energía del nivel fundamental, y ya de paso, la del resto de niveles:\[H|0\rangle = \hbar\omega\left(a^\dagger a+\frac{1}{2}\right)|0\rangle = \frac{1}{2}\hbar\omega |0\rangle\]
Ahora los estados excitados los podemos obtener aplicando sucesivamente el operación creación (y normalizando adecuadamente) sobre el fundamental:
\[|n\rangle = \frac{1}{\sqrt{n!}}{a^\dagger}^n|0\rangle \qquad H|n\rangle = \hbar\omega\left(n+\frac{1}{2}\right)|n\rangle\]
¿Y ahora qué?
Las teorías físicas más fundamentales no describen el universo en términos de ondas y/o corpúsculos, sino con campos. Y un campo no es más que un conjunto de (infinitos) osciladores de distintas frecuencias. El estado fundamental es el vacío, y sus excitaciones son las partículas. Y los operadores de creación y destrucción, pues eso, crean y destruyen partículas. Por ejemplo, al cuantizar al campo electromagnético \(A_\mu\), los estados excitados corresponden a los fotones.
En un caso más aplicado, los osciladores cuánticos también son relevantes en la física del estado sólido. En un sólido, los átomos vibran en torno a unas posiciones fijas que determinan la red cristalina. La oscilación se produce de manera acoplada: el movimiento se puede describir como una superposición de modos normales (cada uno asociado con un oscilador), patrones en los que todos los átomos del sólido se mueven acompasadamente. Al cuantizar los modos normales, las excitaciones de los osciladores se denominan fonones (con n, no con t. El nombre se debe a que los fonones de baja frecuencia son los responsables de la transmisión del sonido, en griego phonos). Los fonones se comportan en muchas situaciones como auténticas partículas: sufren emisión, absorción, dispersión,... (son cuasipartículas). Este tipo de procesos determina algunas propiedades macroscópicas de los sólidos, como el calor específico o la dilatación térmica. En los sólidos existen también otras oscilaciones, que dan lugar a más cuasipartículas como los plasmones (oscilaciones del gas de electrones) o los magnones (oscilaciones de los espines de los electrones).
Para saber más
Enrique Borja va a comenzar próximamente una serie de entradas dedicadas al oscilador armónico (The Physics Tour '15). Hasta entonces, también puedes echar un vistazo a sus entradas: La joya de la corona: El oscilador armónico (básico), El oscilador armónico cuántico 1ª parte, Reto ¿te atreves?Un poco de malabarismo matemático, Reto II: Otra vez el oscilador armónico. ¿Por qué no?, Oscilones,

No hay comentarios:
Publicar un comentario