Bosoneando: Nadando con flagelos

Surcando por las olas de internet, el otro día di con una página llamada Stack Exchange - WorldBuilding. Es un foro de preguntas y respuestas que tratan sobre la construcción de mundos literarios alternativos. En particular llamó mi atención una pregunta sobre la posibilidad de animales marinos que se desplazaran usando movimienros rotatorios de un modo similar a un sacacorchos.

La respuesta es que, para un animal (es decir, algo con un tamaño de milímetros o mayor), sería una forma de desplazamiento terriblemente poco eficiente, ya que el movimiento de cada segmento del sacacorchos se produce en una dirección prácticamente perpendicular al desplazamiento neto. Los movimientos que realizan los animales marinos que todos conocemos requieren mucha menos energía. Obviamente una reducción del gasto de energía siempre es una ventaja evolutiva. Esto unido a la dificultad de mantener estructuras biológicas rotatorias hace altamente improbables a los animales imaginados por el usuario del sitio.

Cariño, he encogido a los bichos

Os habréis fijado que en el párrafo anterior he puesto énfasis en el tamaño que tiene un animal. Y es que las cosas no siempre escalan como esperaríamos.

En primer lugar, hay que tener en cuenta que, al moverse por cualquier fluído, aparece una fuerza de rozamiento viscoso \[F_v \sim -\eta L v\] Así pues, al aplicar una fuerza externa el balance de fuerzas es \[F_{ext} - \eta v = m a\]

Podemos definir el número de Reynolds como cociente entre fuerzas inerciales y viscosas (es por tanto una magnitud adimensional). Si la dimensión del objeto es \(L\) y se meuve con velocidad \(v\) por un fluido con densidad \(\rho\), las fuerza inercial se puede aproximar como \[ma \approx \rho L^3 \frac{v^2}{L} \qquad \] Por lo que el número de Reynolds es \[Re = \frac{ma}{\eta L v} = \frac{\rho L v}{\eta}\]Si el número de Reynolds es grande, se produce un flujo turbulento, y en caso contrario un flujo laminar. Pero lo más importante es que, si es extremadamente bajo, se puede despreciar por completo el término inercial \(ma\) (régimen sobreamortiguado):\[F_{ext} = \eta L v = \xi v\]Empleando un mismo fluído, por ejemplo el agua, el número de Reynolds cambia drásticamente con la escala de longitudes \(L\) considerada. Así, mientras que para Michael Phelps o para una piraña el agua es un medio en el que se pueden mover con inercia como pez en el agua, para una bacteria la vida es bien distinta: para ella, nadar es tan complicado (o más) como para nosotros hacerlo en miel.

Cuando tú vas, yo vengo de allí

Hemos eliminado la inercia del movimiento, ¿y eso qué consecuencias tiene? Comparando las ecuaciones del régimen sobreamortuguado con la segunda ley de Newton de toda la vida, la principal diferencia es que en una salen derivadas primeras respecto al tiempo y en otra derivadas segundas. Si hacemos, por lo tanto, una inversión en el tiempo \(t \to -t\), la derivada cambia de signo, por lo que la fuerza también lo hace. Dicho de otro modo: a bajo número de Reynolds, mover una aleta hacia alante y hacia atrás lo único que consigue es llevarte a la casilla de salida, porque el movimiento hacia atrás (independientemente de su velocidad) deshace el efecto del movimiento hacia alante, al contrario de lo que ocurriría en el caso inercial. Edward Purcell llamó a esto el Teorema de la almeja.

Para evitar quedarse atascado, un ser que se mueva a bajo número de Reynolds necesita describir un movimiento que no sea equivalente al verlo hacia atrás en el tiempo. Purcell hizo algunas propuestas ingeniosas, como un animal con dos aletas que se muevan de forma desacompasada o un ser toroidal que mueva su superficie. La naturaleza se ha decantado por soluciones más simples, como los cilios y los flagelos.

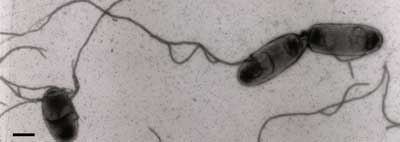
Los flagelos de algunas bacterias, como la famosa Escherichia Coli, son básicamente los sacacorchos que proponía al principio: un largo filamento helicoidal rotatorio (cuidado, otras células usan sus flagelos de formas diferentes, como por ejemplo ondeándolo). La rotación del flagelo se debe a que está unido a una proteína de membrana, la ATPasa, que produce movimiento rotatorio aprovechando el flujo de protones debido a un gradiente de concentración.

Como una imagen vale más que mil palabras, aquí os dejo un vídeo demostrando las dificultades para nadar en bajo número de Reynolds. La parte relevante empieza en 4:58. (El vídeo es de Sir Geoffrey Taylor, y aunque tiene unos añitos, es bastante espectacular)