Un sólido es una colección de (idealmente infinitos) átomos que siguen un patrón que se repite regularmente tras una distancia \(a\) (parámetro de red) - vamos a considerar cristales unidimensionales. Para el caso tridimensional, todo es igual solo que con vectores-. Por lo tanto, el potencial que sufren los electrones por encontrarse en la red también presentará esa periodicidad \[U(x+R) = U(x) \qquad R = n a \]
Esto otorga a las funciones de onda de los electrones una forma muy especial, dada por el teorema de Bloch (teorema de Floquet si hay algún matemático leyendo esto) \[\psi_k(x) = e^{ikx} u_k (x) \qquad u_k(x+R) = u_k(x)\] Por supuesto podéis confiar en mi palabra (y la de Bloch y Floquet) de que esto es cierto. Pero en caso de que seais unos descreídos, ahí va una demostración
\begin\(\{\)demostration\(\}\)
Usaremos el operador de traslación \(T_R f(x) = f(x+R)\), que debe ser unitario. Como el potencial (y por tanto el hamiltoniano) son invariantes al desplazarlos una distancia \(R\), \(H(x+R) = H(x)\), entonces \[T_R H(x) \psi(x) = H(x+R) \psi(x+R) = H(x) \psi(x+R) = H(x) T_R \psi (x)\] de donde se deduce que \[ [H, T_R] = 0\] Esto nos garantiza que podemos encontrar funciones que sean simultáneamente autoestados de \(H\) y de \(T_R\): \[H\psi(x) = \varepsilon \psi(x) \qquad T_R\psi(x) = c(R)\psi(x)\]El hecho de que el operador de traslación sea unitario implica que \(c(R)= e^{ikR}\). \[\psi_k (x+R) = T_R\psi_k(x) = e^{ikR}\psi_k (x)\] Ahora definimos \( u_k(x) = e^{-ikx} \psi_k(x)\), y podemos comprobar que esta función es periódica con la red: \[u_k(x+R) = e^{-ikx}e^{-ikR}\psi_k(x+R) = e^{-ikx}e^{-ikR}e^{ikR}\psi_k(x) = e^{-ikx} \psi_k(x) = u_k(x)\] y finalmente, de la definición de \(u_k\) tenemos que \[\psi_k(x) = e^{ikx} u_k(x)\]
\end\(\{\)demostration\(\}\)
A \(k\) se la conoce como cuasimomento cristalino, ya que, como veremos al final, aunque no sea el momento del electrón, hace algunas funciones similares, pero eso lo veremos más adelante. Ahora tenemos que elegir qué valores de \(k\) empleamos. Es fácil comprobar que las \(k\) también presentan periodicidad, \(e^{ikR} = e^{i(k+2\pi/a)R}\) . Esto nos permite restringirnos a \(-\frac{\pi}{a} \leq k \leq \frac{\pi}{a}\) (un rinconcito del espacio recíproco conocido como primera zona de Brillouin). En un cristal infinito serían posibles todos esos valores, pero en un cristal finito con \(N\) sitios de red, (con las condiciones de contorno de Born-von Karman, es decir, los dos extremos del cristal son equivalentes) solo existen \(N\) valores posibles, equiespaciados.
El hecho de que la energía, para un valor fijo de \(n\), sea continua y periódica en función de \(k\) implica que tenga un valor mínimo y un máximo. Al rango de energías comprendido entre estos dos extremos lo llamaremos banda de energía.
En general, la estructura de bandas de un material, aun conociendo el potencial que sufren los electrones, es una cuestión bastante complicada, y para ello se usan técnicas como la DFT (Density Functional Theory). A la hora de hacer cálculos con lápiz y papel, se suelen emplear dos aproximaciones contrapuestas: o bien suponer que el potencial de la red es muy pequeño, o que es muy grande.
Si en la red no hubiera potencial, la energía de las bandas tendría una forma parabólica, ya que los electrones están libres. La existencia de distintas bandas se debe al plegado de \(k\) a la primera zona de Brillouin: \[\varepsilon_n(k) = \frac{\hbar^2}{2m}(k-2\pi n/a)^2\]Si el potencial no es nulo pero sí muy débil -modelo NFE, Nearly Free Electrons -, entonces se puede tratar como una corrección al resultado ya conocido, mediante la técnica de teoría de perturbaciones. El resultado es que la mayor modificación se produce en las proximidades del límite de la zona de Brillouin \(k \approx \pm \frac{\pi}{a}\). Allí antes coincidían los límites de dos bandas consecutivas, pero ahora se ha creado una separación entre ambas llamada gap.
Con el enfoque opuesto, consideramos que el potencial es tan intenso - modelo de Tight-Binding - que las energías de los electrones corresponden a los niveles electrónicos de los átomos. Sin embargo, la periodicidad de la red tiene el efecto, además de desplazar los niveles, de ensancharlos debido a la dependencia de la energía con \(k\): así aparecen las bandas de energía, entre las cuales existen importantes gaps creados por la separación de los niveles atómicos.
Vamos a empezar por obtener la ecuación que siguen las funciones \(u_{n,k}(x)\), para ello sustituimos en la ecuación de Schrödinger:\[\left(\frac{\hbar^2}{2m}\frac{d^2}{dx^2} + U\right) e^{ikr} u_{n,k}(x)= e^{ikx}\left[\frac{\hbar^2}{2m} \left(-\frac{d^2}{dx^2}+ k^2\right) -i\frac{\hbar^2}{m}k \frac{d}{dx} + U\right] u_{n,k}(x) = \]\[e^{ikx}H_k u_{n,k}(x) \]
Ahora vamos a hacer una pequeña modificación al cuasimomento \(k \to k+q\): \[H_{k+q} = \frac{\hbar^2}{2m} \left(-\frac{d^2}{dx^2}+ (k+q)^2\right) -i \frac{\hbar^2}{m}(k+q) \frac{d}{dx} + U = H_k + \frac{\hbar^2 q^2}{2m} + \frac{\hbar^2}{m}q\left(k - i\frac{d}{dx}\right)\]
Según la teoría de perturbaciones, si \(q\) es pequeño en comparación con \(k\), la energía se puede expresar como: \[\varepsilon_n(k+q) = \varepsilon_n(k) + \langle n k| \frac{\hbar^2 q^2}{2m} + \frac{\hbar^2}{m}q\left(k - i\frac{d}{dx}\right) |n k \rangle + \sum_{n'\neq n} \frac{|\langle n k| \frac{\hbar^2 q^2}{2m} + \frac{\hbar^2}{m}q\left(k - i\frac{d}{dx}\right) |n' k \rangle|^2}{\varepsilon_n(k) - \varepsilon_{n'}(k)} =\]\[= \varepsilon_n(k) + \frac{\hbar^2}{m} q \langle n k|k - i \frac{d}{dx}|n k \rangle + \frac{\hbar^2 q^2}{2m} + \frac{\hbar^2}{2m} q^2\sum_{n'\neq n} \frac{|\langle n k| -i \frac{d}{dx} |n' k\rangle|^2}{\varepsilon_n(k) - \varepsilon_{n'}(k)} \]
Hemos despreciado los términos que contienen \(q^3\) o potencias superiores. Para el segundo sumando, podemos encontrar una expresión más simple: \[\frac{\hbar^2}{m} q \langle n k|k - i \frac{d}{dx}|n k \rangle = \frac{\hbar^2}{m} \int dx u^\star_{nk} \left(k - i\frac{d}{dx}\right) u_{nk} = \frac{\hbar^2}{m}\int dx \psi^\star_{nk} \left( - i\frac{d}{dx}\right) \psi_{nk} =\]\[ \frac{\hbar p}{m} = \hbar v \]
Los otros dos sumandos, que acompañan a \(q^2\), los metemos debajo de la manta en un parámetro que llamaremos masa efectiva \(m^*\) [nota: en un sólido tridimensional no tiene por qué ser igual en todas las dimensiones, en ese caso estaríamos ante un tensor de masa efectiva m_{ij}^*]. Según la estructura de bandas, la masa efectiva puede ser mayor o menor que la de un electrón, e incluso hacerse negativa en la parte superior de la banda:
\[\frac{1}{m^*} = \frac{1}{m} + \frac{2 \hbar^2}{m}\sum_{n'\neq n} \frac{|\langle n k| -i \frac{d}{dx} |n' k\rangle|^2}{\varepsilon_n(k) - \varepsilon_{n'}(k)}\]
De este modo, la energía finalmente resulta ser \[\varepsilon_n (k+q) = \varepsilon_n (k) + \hbar q v + \frac{\hbar^2 q^2}{2m^*}\]Si te encuentras con la forma funcional de la estructura de bandas -¿quién no se ha encontrado alguna vez con una, que se le haya caído al suelo a un físico despistado? - la forma de calcular los dos parámetros de nuestro modelo es \[v = \frac{1}{\hbar}\frac{d \varepsilon_n (k)}{d k} \qquad \frac{1}{m^*} = \frac{1}{\hbar^2}\frac{d^2 \varepsilon_n (k)}{d k^2} \]
La ventaja de esta aproximación es que la dinámica de los electrones ahora se rige por las ecuaciones de Newton, solo que empleando la velocidad y la masa efectiva que hemos obtenido: \[F = \hbar\dot{\vec{k}}\]
Esto otorga a las funciones de onda de los electrones una forma muy especial, dada por el teorema de Bloch (teorema de Floquet si hay algún matemático leyendo esto) \[\psi_k(x) = e^{ikx} u_k (x) \qquad u_k(x+R) = u_k(x)\] Por supuesto podéis confiar en mi palabra (y la de Bloch y Floquet) de que esto es cierto. Pero en caso de que seais unos descreídos, ahí va una demostración
\begin\(\{\)demostration\(\}\)
Usaremos el operador de traslación \(T_R f(x) = f(x+R)\), que debe ser unitario. Como el potencial (y por tanto el hamiltoniano) son invariantes al desplazarlos una distancia \(R\), \(H(x+R) = H(x)\), entonces \[T_R H(x) \psi(x) = H(x+R) \psi(x+R) = H(x) \psi(x+R) = H(x) T_R \psi (x)\] de donde se deduce que \[ [H, T_R] = 0\] Esto nos garantiza que podemos encontrar funciones que sean simultáneamente autoestados de \(H\) y de \(T_R\): \[H\psi(x) = \varepsilon \psi(x) \qquad T_R\psi(x) = c(R)\psi(x)\]El hecho de que el operador de traslación sea unitario implica que \(c(R)= e^{ikR}\). \[\psi_k (x+R) = T_R\psi_k(x) = e^{ikR}\psi_k (x)\] Ahora definimos \( u_k(x) = e^{-ikx} \psi_k(x)\), y podemos comprobar que esta función es periódica con la red: \[u_k(x+R) = e^{-ikx}e^{-ikR}\psi_k(x+R) = e^{-ikx}e^{-ikR}e^{ikR}\psi_k(x) = e^{-ikx} \psi_k(x) = u_k(x)\] y finalmente, de la definición de \(u_k\) tenemos que \[\psi_k(x) = e^{ikx} u_k(x)\]
\end\(\{\)demostration\(\}\)
A \(k\) se la conoce como cuasimomento cristalino, ya que, como veremos al final, aunque no sea el momento del electrón, hace algunas funciones similares, pero eso lo veremos más adelante. Ahora tenemos que elegir qué valores de \(k\) empleamos. Es fácil comprobar que las \(k\) también presentan periodicidad, \(e^{ikR} = e^{i(k+2\pi/a)R}\) . Esto nos permite restringirnos a \(-\frac{\pi}{a} \leq k \leq \frac{\pi}{a}\) (un rinconcito del espacio recíproco conocido como primera zona de Brillouin). En un cristal infinito serían posibles todos esos valores, pero en un cristal finito con \(N\) sitios de red, (con las condiciones de contorno de Born-von Karman, es decir, los dos extremos del cristal son equivalentes) solo existen \(N\) valores posibles, equiespaciados.
Las bandas y sus gaps
Dado un valor de \(k\), se pueden construir infinitas funciones de onda \(\psi_k(x)\) que son autoestados del hamiltoniano. Las distinguiremos con un índice \(n\), elegido de modo que \(\psi_{n, k}(x) = \psi_{n, k+2\pi/a}(x)\). Por lo tanto:\[\left. \begin{array}{r}H \psi_{n,k}(x) = \varepsilon_n(k) \psi_{n,k}(x) = \varepsilon_n (k) \psi_{n, k+2\pi/a}(x)\\ H \psi_{n, k+2\pi/a} = \varepsilon_n(k +2\pi/a)\psi_{n, k+2\pi/a}(x) \end{array}\right\}\varepsilon_n(k +2\pi/a) = \varepsilon_n(k) \]El hecho de que la energía, para un valor fijo de \(n\), sea continua y periódica en función de \(k\) implica que tenga un valor mínimo y un máximo. Al rango de energías comprendido entre estos dos extremos lo llamaremos banda de energía.
En general, la estructura de bandas de un material, aun conociendo el potencial que sufren los electrones, es una cuestión bastante complicada, y para ello se usan técnicas como la DFT (Density Functional Theory). A la hora de hacer cálculos con lápiz y papel, se suelen emplear dos aproximaciones contrapuestas: o bien suponer que el potencial de la red es muy pequeño, o que es muy grande.
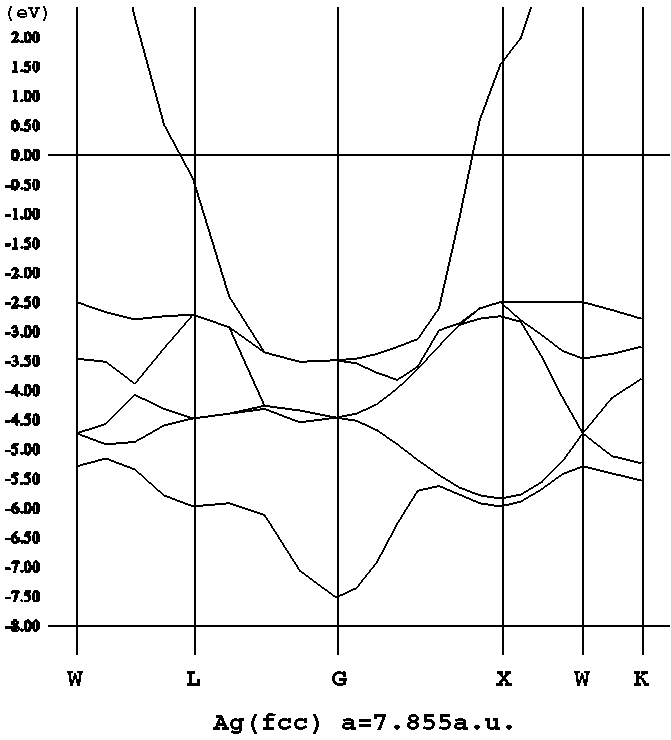 |
| Bandas electrónicas en la plata |
Si en la red no hubiera potencial, la energía de las bandas tendría una forma parabólica, ya que los electrones están libres. La existencia de distintas bandas se debe al plegado de \(k\) a la primera zona de Brillouin: \[\varepsilon_n(k) = \frac{\hbar^2}{2m}(k-2\pi n/a)^2\]Si el potencial no es nulo pero sí muy débil -modelo NFE, Nearly Free Electrons -, entonces se puede tratar como una corrección al resultado ya conocido, mediante la técnica de teoría de perturbaciones. El resultado es que la mayor modificación se produce en las proximidades del límite de la zona de Brillouin \(k \approx \pm \frac{\pi}{a}\). Allí antes coincidían los límites de dos bandas consecutivas, pero ahora se ha creado una separación entre ambas llamada gap.
 |
| Bandas de energía con potencial nulo (izquierda) y en aproximación NFE (derecha) |
Con el enfoque opuesto, consideramos que el potencial es tan intenso - modelo de Tight-Binding - que las energías de los electrones corresponden a los niveles electrónicos de los átomos. Sin embargo, la periodicidad de la red tiene el efecto, además de desplazar los niveles, de ensancharlos debido a la dependencia de la energía con \(k\): así aparecen las bandas de energía, entre las cuales existen importantes gaps creados por la separación de los niveles atómicos.
Teorema de la masa efectiva
Una vez que tenemos los electrones acomodados en bandas de energía, cabe preguntarnos cómo responderán si les hacemos alguna perrería, tal como aplicarles un campo eléctrico o magnético. Obviamente la dependencia de la energía con \(k\) puede ser muy complicada, y por supuesto habrá que tratar las fuerzads aplicadas dentro del formalismo cuántico. Afortunadamente, podemos realizar aproximaciones que sean válidas con gran generalidad, y que como bonus, nos reduzcan las ecuaciones a unas que tengan toda la pinta de ser clásica.Vamos a empezar por obtener la ecuación que siguen las funciones \(u_{n,k}(x)\), para ello sustituimos en la ecuación de Schrödinger:\[\left(\frac{\hbar^2}{2m}\frac{d^2}{dx^2} + U\right) e^{ikr} u_{n,k}(x)= e^{ikx}\left[\frac{\hbar^2}{2m} \left(-\frac{d^2}{dx^2}+ k^2\right) -i\frac{\hbar^2}{m}k \frac{d}{dx} + U\right] u_{n,k}(x) = \]\[e^{ikx}H_k u_{n,k}(x) \]
Ahora vamos a hacer una pequeña modificación al cuasimomento \(k \to k+q\): \[H_{k+q} = \frac{\hbar^2}{2m} \left(-\frac{d^2}{dx^2}+ (k+q)^2\right) -i \frac{\hbar^2}{m}(k+q) \frac{d}{dx} + U = H_k + \frac{\hbar^2 q^2}{2m} + \frac{\hbar^2}{m}q\left(k - i\frac{d}{dx}\right)\]
Según la teoría de perturbaciones, si \(q\) es pequeño en comparación con \(k\), la energía se puede expresar como: \[\varepsilon_n(k+q) = \varepsilon_n(k) + \langle n k| \frac{\hbar^2 q^2}{2m} + \frac{\hbar^2}{m}q\left(k - i\frac{d}{dx}\right) |n k \rangle + \sum_{n'\neq n} \frac{|\langle n k| \frac{\hbar^2 q^2}{2m} + \frac{\hbar^2}{m}q\left(k - i\frac{d}{dx}\right) |n' k \rangle|^2}{\varepsilon_n(k) - \varepsilon_{n'}(k)} =\]\[= \varepsilon_n(k) + \frac{\hbar^2}{m} q \langle n k|k - i \frac{d}{dx}|n k \rangle + \frac{\hbar^2 q^2}{2m} + \frac{\hbar^2}{2m} q^2\sum_{n'\neq n} \frac{|\langle n k| -i \frac{d}{dx} |n' k\rangle|^2}{\varepsilon_n(k) - \varepsilon_{n'}(k)} \]
Hemos despreciado los términos que contienen \(q^3\) o potencias superiores. Para el segundo sumando, podemos encontrar una expresión más simple: \[\frac{\hbar^2}{m} q \langle n k|k - i \frac{d}{dx}|n k \rangle = \frac{\hbar^2}{m} \int dx u^\star_{nk} \left(k - i\frac{d}{dx}\right) u_{nk} = \frac{\hbar^2}{m}\int dx \psi^\star_{nk} \left( - i\frac{d}{dx}\right) \psi_{nk} =\]\[ \frac{\hbar p}{m} = \hbar v \]
Los otros dos sumandos, que acompañan a \(q^2\), los metemos debajo de la manta en un parámetro que llamaremos masa efectiva \(m^*\) [nota: en un sólido tridimensional no tiene por qué ser igual en todas las dimensiones, en ese caso estaríamos ante un tensor de masa efectiva m_{ij}^*]. Según la estructura de bandas, la masa efectiva puede ser mayor o menor que la de un electrón, e incluso hacerse negativa en la parte superior de la banda:
\[\frac{1}{m^*} = \frac{1}{m} + \frac{2 \hbar^2}{m}\sum_{n'\neq n} \frac{|\langle n k| -i \frac{d}{dx} |n' k\rangle|^2}{\varepsilon_n(k) - \varepsilon_{n'}(k)}\]
De este modo, la energía finalmente resulta ser \[\varepsilon_n (k+q) = \varepsilon_n (k) + \hbar q v + \frac{\hbar^2 q^2}{2m^*}\]Si te encuentras con la forma funcional de la estructura de bandas -¿quién no se ha encontrado alguna vez con una, que se le haya caído al suelo a un físico despistado? - la forma de calcular los dos parámetros de nuestro modelo es \[v = \frac{1}{\hbar}\frac{d \varepsilon_n (k)}{d k} \qquad \frac{1}{m^*} = \frac{1}{\hbar^2}\frac{d^2 \varepsilon_n (k)}{d k^2} \]
La ventaja de esta aproximación es que la dinámica de los electrones ahora se rige por las ecuaciones de Newton, solo que empleando la velocidad y la masa efectiva que hemos obtenido: \[F = \hbar\dot{\vec{k}}\]

No hay comentarios:
Publicar un comentario