Bosoneando: Ondas por doquier

¿Qué haces, insensato? ¿Acaso no sabes que te estás poniendo en grave riesgo al leer esto? Si estas usando wifi, 3G o 4G para conectarte a internet y leer este blog, será mejor que dejes de hacerlo y te vayas a una caverna a pintar pinturas paleolíticas. Así te podrás proteger del peligro que suponen las ondas electromagnéticas. Así nos lo advertía, en Informativos Telecinco, un "experto" blandiendo un detector de ondas que chasqueaba más que un detector Geiger en la puerta de Fukushima (por cierto, me gustaría ver la cara que habrán puesto los redactores del informativo al enterarse de que para emitir semejante reportaje han emitido cantidades ingentes de las perniciosas ondas electromagnéticas).

Electromagnetic fields forever

La electricidad y el magnetismo fueron dos fenómenos que resultaban misteriosos y desconocidos hasta la síntesis en el siglo XIX de sus principios básicos, que culminó con la formulación de las cuatro leyes de Maxwell (aunque Maxwell solo formuló una de ellas, tuvo el mérito de reconocer la importancia de las leyes en su conjunto. Por cierto, cumplen su 150º aniversario). Para ello hizo falta introducir el campo eléctrico \(\vec{E}\) y el campo magnético \(\vec{B}\). Un campo es una magnitud que toma un valor en cada punto del espacio (y el tiempo), y en este caso son campos vectoriales, por lo que la magnitud en cuestión es un vector, es decir, está caracterizada por su sentido además de por su intensidad. Las ecuaciones de Maxwell establecen las relaciones entre sus variaciones en el espacio y el tiempo:

\(\vec{\nabla}\cdot \vec{E} = \frac{\rho}{\varepsilon} \qquad \vec{\nabla}\cdot\vec{B} = 0 \qquad \vec{\nabla}\times\vec{E} = - \frac{\partial \vec{B}}{\partial t}\qquad \vec{\nabla}\times\vec{B} = \mu\vec{J} + \mu\varepsilon\frac{\partial \vec{E}}{\partial t}\)

¿Qué nos están queriendo decir estas ecuaciones? Para empezar, apuntan directamente a los culpables: los campos eléctricos y magnéticos están generadas por cargas eléctricas \(\rho\) y corrientes eléctricas \(\vec{J}\) (¿nadie echa de menos a cargas y corrientes magnéticas?...). Pero hay más escondido. Si nos situamos en una región donde no haya cargas (\(\rho=0\), \(\vec{J}=0\)), pero por algún motivo haya un campo magnético que cambie con el tiempo, la cuarta ecuación crea un campo magnético que también dependerá en el tiempo, a lo que la tercera ecuación responde creando un campo eléctrico variable, que a su vez por la cuarta ecuación, etc etc... Así hemos conseguido que el campo eléctrico inicial se propague en el espacio. Las dos primeras ecuaciones fuerzan a que el campo eléctrico y el magnético sean perpendiculares entre sí y a la dirección de propagación (estrictamente esto solo es cierto en el vacío). Matemáticamente, se pueden combinar las cuatro ecuaciones en ausencia de cargas para dar la conocida ecuación de ondas

\(\nabla^2 \vec{E} = \frac{1}{v^2} \frac{\partial^2 \vec{E}}{\partial t}\)

En esta ecuación, \(v\) es la propagación de la onda. En el caso de encontrarnos en el vacío (el aire, a efectos electromagnéticos, se puede considerar como el vacío), esta velocidad es una constante universal, \(c = 299792458\)m/s.

Cualquier solución a esta ecuación se puede escribir como una suma de ondas planas, de la forma

\(\vec{E}(\vec{x}, t) = \vec{E_0}\cos(\vec{k}\cdot\vec{x} - \omega t + \phi)\)

Los parámetros de la onda son el vector de ondas \(\vec{k}\) y la frecuencia \(\omega\). El vector de ondas apunta en la dirección de propagación de la onda, e indica la periodicidad espacial de la onda: El campo eléctrico es igual al desplazarse una distancia \(\lambda = \frac{2\pi}{|\vec{k}|}\) en la dirección de propagación. Del mismo modo, la frecuencia proporciona la periodicidad temporal de la onda \(T = \frac{2\pi}{\omega}\). Frecuencia y vector de ondas no son independientes, sino que están ligados por la relación de dispersión \(\omega(\vec{k})\). En el caso de ondas electromagnéticas en el vacío, es tan simple como

\(\omega(\vec{k}) = c |\vec{k}|\)

De colores se visten los campos en la primavera

La frecuencia puede variar enormemente de unas ondas electromagnéticas a otras. Esta diversidad conforma lo que se conoce como el espectro electromagnético. La región más familiar es el visible, porque nuestros ojos la pueden detectar. El color es una medida, un tanto tosca, de la frecuencia de estas radiaciones: el rojo es la luz visible con una frecuencia menor, y el violeta la de mayor frecuencia. A mayores frecuencias que el visible se encuentran los ultravioletas, y despuás los rayos X y los rayos \(\gamma\). Menores frecuencias que el visible tienen los infrarrojos, las microondas y las ondas de radio. Es útil pensar en longitudes de onda, ya que dan una idea del "tamaño efectivo" de la onda, y por tanto, del tamaño de los objetos con los que puede interaccionar. Así, las ondas de radio tienen una longitud de varios metros, las microondas de centímetros, la luz visible entre 400nm y 700nm, y los rayos X corresponden a unos pocos angstrom.

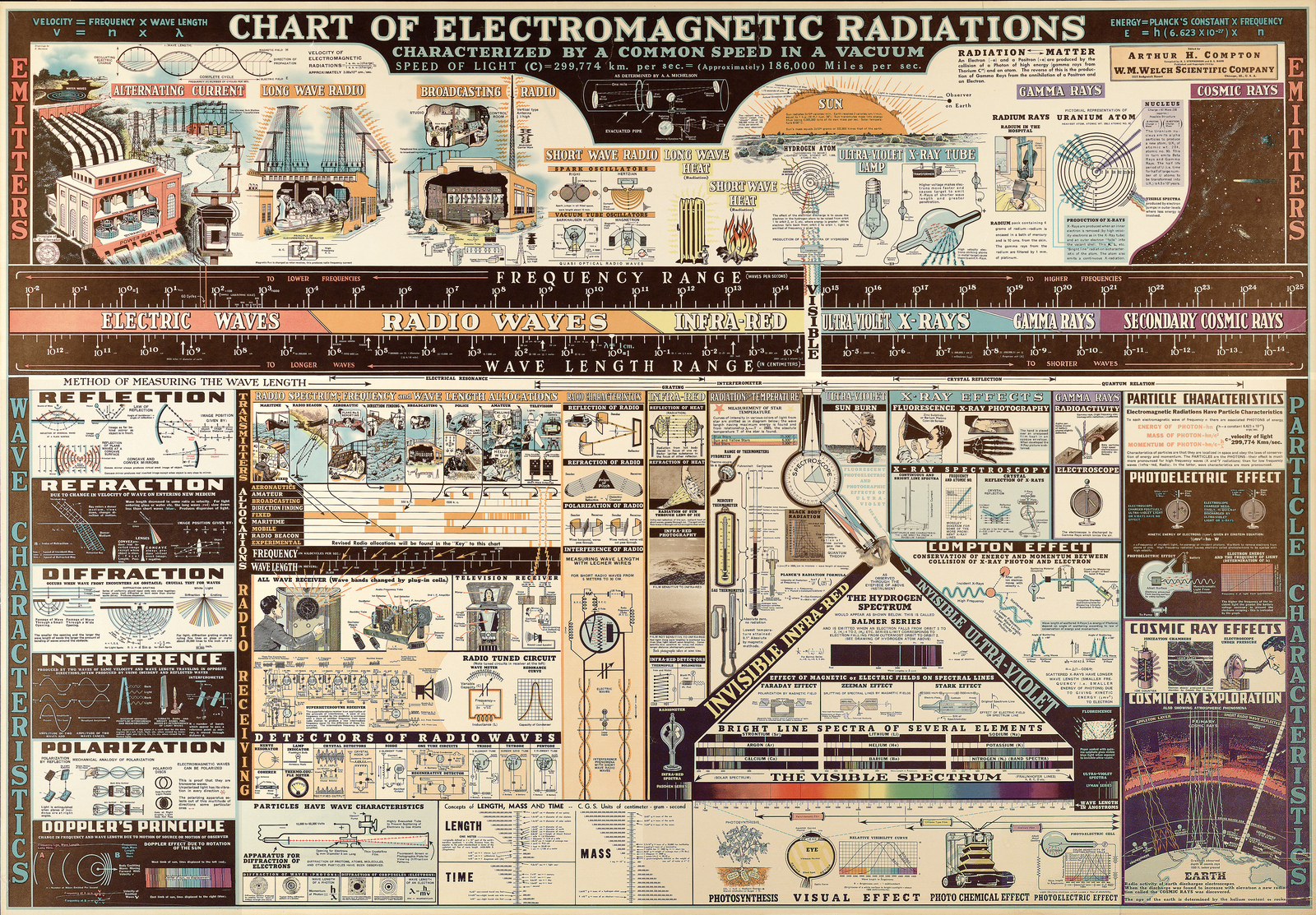El espectro electromagnético, según Lawrence Livermore National Labs

Las ondas electromagnéticas transportan energía \(\mathcal{E} = \frac{1}{2}\varepsilon |\vec{E}|^2\) y momento lineal \(|\vec{p}| = \frac{\mathcal{E}}{c}\). Uno de los descubrimientos que dieron lugar a la revolución de la cuántica es que las ondas no pueden ganar o perder cantidades arbitrarias de energía, solamente lo pueden hacer en múltiplos enteros de los cuantos (fotones) de energía, proporcionales a la frecuencia \(\Delta \mathcal{E} = h \nu\). Para las radiaciones de baja frecuencia, el efecto de la cuantización es poco relevante ya que siempre se intercambia un número enorme de fotones, pero a altas frecuencias la naturaleza discreta de la luz se hace evidente.

¡Peligro!

La peligrosidad de las diferentes ondas electromagnéticas está determinada por su frecuencia y su intensidad.

Para frecuencias relativamente bajas (entre 10 y 100MHz), el efecto principal es el calentamiento dieléctrico: las moléculas polares se alinean con el campo eléctrico, y como éste oscila, las moléculas se mueven lo que conlleva un aumento de la temperatura (este es el mecanismo por el que funcionan los hornos microondas).

En el rango visible, como poseedores de unos sensores de radiación (los ojos), hay que tomar las precauciones necesarias: la exposición a fuentes de luz intensa como un láser o el Sol sin protección pueden provocar graves daños.

La radiación ultravioleta y los rayos X suponen riesgos debido a que son ionizantes: la energía de uno de sus fotones es suficientemente alta para romper los enlaces químicos y formar otros nuevos. El mayor peligro lo corren las moléculas de ADN (o DNA, según los gustos), ya que puede provocar que dos bases pirimidínicas de la misma cadena se unan por un enlace covalente. Las células tienen mecanismos de reparación capaces de localizar estos dímeros, pero si pasa desapercibida, en la siguiente replicación del material genético puede causar una mutación. Esta mutación puede originar un cáncer (o enfados viscerales y coloración verdosa de la piel, como le pasa al pobre Bruce Banner).

En el caso que aparece en el reportaje de los informativos, todas las radiaciones que nuestro experto analiza son microondas, por lo que el único efecto que pueden provocar sobre la salud es el calentamiento. Naturalmente, los dispositivos electrónicos (teléfonos móviles, wifi) operan a intensidades muy bajas: un móvil emite típicamente 1W, con lo que tendría que calentar toda una habitación, mientras que un horno microondas necesita al menos 700W para calentar el pequeño receptáculo en el que metes tu comida. Así que, con un uso responsable, el calentamiento dieléctrico no debería ser un motivo de preocupación (y no lo digo solo yo, si no pregúntaselo a Clara Grima).

Un tema recurrente en los informativos es la supuesta conexión entre las ondas de radiofrecuencia y el cáncer. Pese a no contar con ninguna base física, esta teoría es bastante popular. La OMS ha realizado estudios epidemiológicos al respecto, y tampoco ha encontrado una relación de correlación (y correlación no implica causalidad). Por ello cataloga estas radiaciones dentro de la categoría 2B, de sustancias para las cuales no hay suficientes evidencias de su acción carcinógena (incluye, por ejemplo, el café y el talco). Desde el punto de vista físico, es un completo absurdo pensar que las microondas puedan tener tal efecto, por su poca energía y su gran longitud de onda (miles de veces mayor que cualquier célula). Para hacernos una idea, es como intentar tamizar la harina con un filtro cuyos agujeros midieran un metro de largo. Absurdo, ¿no?

Y si hemos descartado los efectos térmicos y los ionizantes, ¿qué nos queda?. En el reportaje se hace referencia a la hipersensibilidad electromagnética, una enfermedad en la que radiaciones electromagnéticas de baja frecuencia e intensidad supuestamente causan problemas de salud como dolores de cabeza o falta de sueño. Las investigaciones al respecto concluyen que, aunque los síntomas sean reales, no muestran ninguna relación con la existencia de radiaciones: en estudios de doble ciego, los pacientes no notan diferencias entre situaciones en presencia o ausencia de las ondas. Los síntomas son tan inespecíficos que podrían tener infinidad de causas. Tal es así que la OMS califica esta enfermedad de idiopática, es decir, de causa desconocida.

En el reportaje se presenta la relación entre la enfermedad y su supuesta causa como algo seguro, sin aportar ningún tipo de evidencias más que una referencia muy de pasada a "los expertos", sin especificar quiénes son esos expertos. Además, cifran el número de enfermos en el 10% de la población española, muchos de los cuales no lo saben. De nuevo no ofrecen ningún estudio que apoye este dato, y lo presentan como un hecho irrebatible, sin decir que es una estimación (por cierto, los estudios hechos al respecto en otros países ofrecen cifras muchísimo menores). El colmo llega cuando el experto acerca su aparatito a una lámpara apagada y muestra la lectura: evidentemente, da un valor del campo eléctrico (bastante pequeño, dicho sea de paso): por supuesto que hay un campo eléctrico, pero si la lámpara está desconectada ¡será un campo estático! ¡no crea ondas, peligrosas o no! En fin, una falta absoluta de rigor y un ejemplo de manual de sensacionalismo.

Pero puede que tengan razón en algo... A mí las ondas electromagnéticas a veces sí me dan dolores de cabeza, cuando se usan para difundir semejante sarta de despropósitos.